矩阵的行列式和逆|flask|六狼博客|技术博客|技术论坛|六狼网络|六狼科技|六狼IT|六狼星球

2025年9月11日

在电影奇异博士里面，空间可以根据能量被无限扭转，以至于在电影院里面看的时候容易晕头转向。这是我们大脑的局限性决定的，但为了描述更复杂的数学问题，数学家往往需要进行高维度的抽象和计算，这也是为什么大学里面的数学开始令人感觉困难的原因。

一、矩阵的意义

在上一篇文章矩阵的计算与应用中，我们了解了矩阵的基本特性和使用场景，但对许多人来说，对矩阵的认识仍然还停留在二维数组上面，而实际上矩阵的几何变换，才是理解线性代数的精髓。

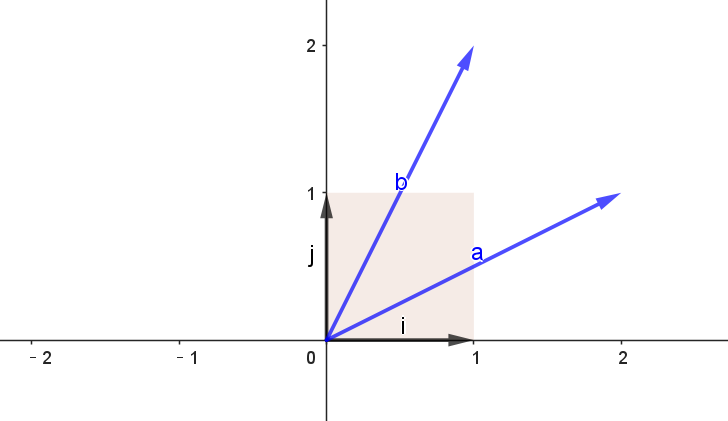
我们先想象你面前有一张无限大的、由完美正方形网格组成的纸。在这个网格上，有两个特殊的向量：一个沿着水平方向的 i 向量 [1,0]，和一个沿着垂直方向的 j 向量 [0,1]。这两个向量构成了我们空间的“基石”，它们围成了一个面积为 1×1=1 的单位正方形，如下图：

向量a[1,0] 和向量 b[0,1]，正好构成了一个2*2的单位矩阵 I：

接下来，我们尝试在这个平面坐标系中绘制两个从原点出发的向量。

向量a[2, 1] 和向量 b[1,2]，正好构成了一个2*2的矩阵 A：

具象的说，一个矩阵可以被看作是一系列指令，它告诉你如何拉伸、旋转、压缩原始坐标网格。

以上面的网格为例，我们假设水平方向的 i 向量 [1,0]经过旋转拉伸变换到了 a[2, 1] ，而垂直方向的 j 向量 [0,1] 经过旋转拉伸变换到了 b[1,2 ]，那么随之而来的，就是整个坐标网格都发生了相同方向和倍数的线性变换，如下所示：

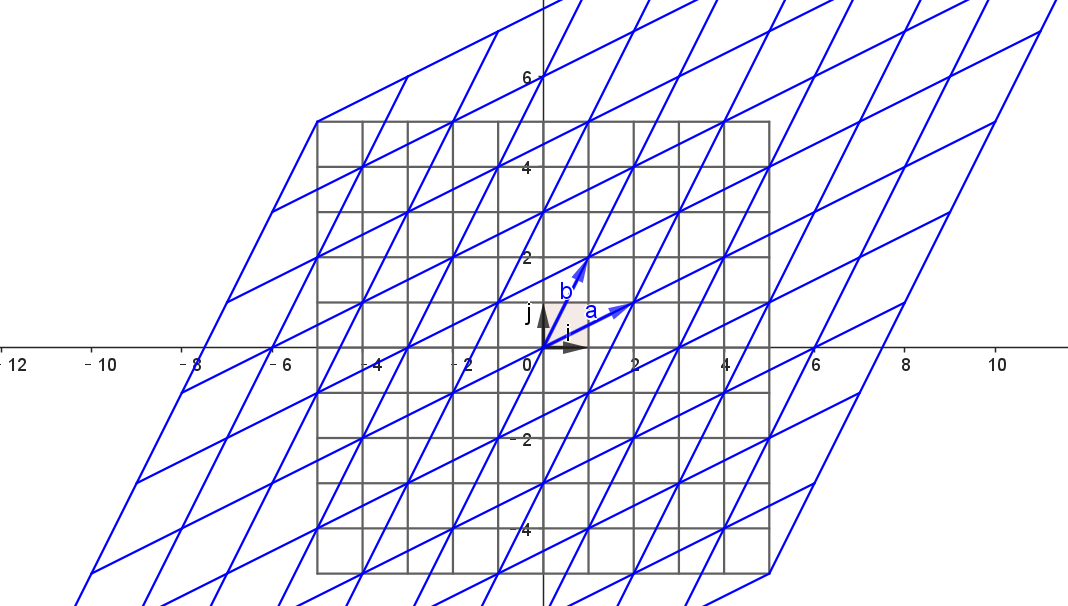
构成矩阵的向量可以告诉我们基石向量 i 和 j 在变换后会移动到哪里，根据线性变换的特点进一步推断出整个空间的形状会如何进行变化。那么如果一个矩阵是 3×3 的，它所代表的线性变换作用于三维空间，矩阵的分向量就代表了对这个三维空间进行变换的一系列指令，这样的变化可以实现三维拉伸或压缩物体的效果，比如把一个球体变成一个椭球体等等。

由此可见，而且无论是平面二维、立体三维或是更高维的计算，都可以借鉴这样的计算方式。

接下来，介绍两个线性变换中的基础概念：

矩阵的行列式：行列式是一个标量值，它描述了坐标网格在变换过程中的缩放因子。通过计算行列式我们可以知道，在经过矩阵向量变换后，图形的面积或体积被缩放了多少倍。
矩阵的逆：我们已知基向量方阵按矩阵向量的方向进行变换（乘积）后可以实现空间变换效果，那么怎么撤销这个变换效果呢？矩阵的逆是一个反向变换的矩阵，通过将矩阵和它的逆矩阵进行乘积运算，可以恢复到基石向量方阵，也就是原来的样子。

二、矩阵的行列式

矩阵行列式，用于描述方块矩阵在线性变换时，关于“体积”的影响因子，或者说是将一个单位“体积”（如单位正方形或单位立方体）进行线性变换后，其体积发生变化的比例。

行列式的计算公式取决于矩阵的大小。

二阶行列式

对于一个二阶矩阵：

\[A = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \]

其行列式记为 $|A|$ 或 $\det(A)$，计算公式为： $ |A| = ad – bc $

例如：

计算矩阵 $A = \begin{pmatrix} 3 & 5 \\ 1 & 4 \end{pmatrix}$ 的行列式。

根据二阶矩阵的公式：

\[ |A| = (3 \times 4) – (5 \times 1) = 12 – 5 = 7 \]

三阶行列式

对于一个三阶矩阵：

\[A = \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix} \]

其行列式可以使用对角线法则（也称为萨吕斯法则）计算：

\[ |A| = a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} – a_{13}a_{22}a_{31} – a_{11}a_{23}a_{32} – a_{12}a_{21}a_{33} \]

例如：

计算矩阵 $B = \begin{pmatrix} 1 & 2 & 3 \\ 0 & 1 & 4 \\ 2 & 0 & 5 \end{pmatrix}$ 的行列式。

使用对角线法则：

\[|B| = (1 \times 1 \times 5) + (2 \times 4 \times 2) + (3 \times 0 \times 0) – (3 \times 1 \times 2) – (1 \times 4 \times 0) – (2 \times 0 \times 5) \]

结果：

\[|B| = 5 + 16 + 0 – 6 – 0 – 0 = 15 \]

N阶行列式

对于大于三阶的方块矩阵，通常使用拉普拉斯展开定理（Laplace Expansion）来计算行列式。

该定理允许我们将一个 n 阶行列式展开为若干个 (n-1) 阶行列式（称为余子式）的线性组合。

我们可以沿着任意一行或任意一列进行展开。以沿着第一行为例，n 阶矩阵 A 的行列式可以表示为：

\[|A| = \sum_{j=1}^{n} (-1)^{1+j} a_{1j} M_{1j} \]

其中：

$a_{1j}$ 是第一行第 j 列的元素。
$M_{1j}$ 是 $a_{1j}$ 的余子式，即去掉矩阵 $A$ 的第一行和第 j 列后得到的 (n-1) 阶子矩阵的行列式。
$(-1)^{1+j} M_{1j}$ 称为 $a_{1j}$ 的代数伴随式。

这个过程可以递归地进行，直到将 n 阶行列式转化为二阶或三阶行列式，然后进行计算。

例如：

计算矩阵 $B = \begin{pmatrix} 1 & 2 & 3 \\ 0 & 1 & 4 \\ 2 & 0 & 5 \end{pmatrix}$ 的行列式。

使用降阶公式分解：

\[|B| = (-1)^{1+1} \cdot 1 \cdot \begin{vmatrix} 1 & 4 \\ 0 & 5 \end{vmatrix} + (-1)^{1+2} \cdot 2 \cdot \begin{vmatrix} 0 & 4 \\ 2 & 5 \end{vmatrix} + (-1)^{1+3} \cdot 3 \cdot \begin{vmatrix} 0 & 1 \\ 2 & 0 \end{vmatrix} \]

计算各个二阶行列式：

$\begin{vmatrix} 1 & 4 \\ 0 & 5 \end{vmatrix} = (1 \times 5) – (4 \times 0) = 5$
$\begin{vmatrix} 0 & 4 \\ 2 & 5 \end{vmatrix} = (0 \times 5) – (4 \times 2) = -8$
$\begin{vmatrix} 0 & 1 \\ 2 & 0 \end{vmatrix} = (0 \times 0) – (1 \times 2) = -2$

代入展开式：

\[|B| = 1 \cdot 1 \cdot 5 + (-1) \cdot 2 \cdot (-8) + 1 \cdot 3 \cdot (-2) \]

结果：

\[|B| = 5 + 16 – 6 = 15 \]

行列式特征

行列式虽然是一个标量，但可以有正负、也可以是零，这代表的是空间”体积”的变化是否发生了反转，或者压扁。

以一个基础的单位正方形和它所在的坐标网格为例，这个单位正方形由两个基向量 [1,0] 和 [0,1] 构成，它的面积是 1。接下来，设定一个 2×2 矩阵观察其如何进行空间变换。

A. 行列式 > 0

当行列式为正时，变换会拉伸或压缩空间，但不会改变空间的朝向（没有翻转）。

我们以矩阵 $A = \begin{pmatrix} 2 & 0 \\ 1 & 1 \end{pmatrix}$ 为例。

变换前： 两个基向量是 [1,0] 和 [0,1]，它们构成了一个面积为 1 的单位正方形。
变换后：
- 第一个基向量 [1,0] 被变换到了 [2,0]。
- 第二个基向量 [0,1] 被变换到了 [1,1]。
结果： 整个网格被拉伸了，并且向右倾斜了（剪切）。原来的单位正方形变成了一个面积为 2 的平行四边形（因为行列式 2×1−1×0=2）。

B. 行列式 < 0

当行列式为负时，变换不仅会拉伸或压缩空间，还会对空间进行翻转。

我们以矩阵 $B = \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix}$为例。

变换前： 两个基向量是 [1,0] 和 [0,1]。
变换后：
- 第一个基向量 [1,0] 被变换到了 [−1,0]。
- 第二个基向量 [0,1] 被变换到了 [0,1]。
结果： 整个网格沿 Y 轴进行了镜像翻转。虽然形状没有改变，但左右方向发生了反转。行列式为 −1（−1×1−0×0=−1），说明面积没有变化，但空间被翻转了。

C. 行列式 = 0

当行列式为零时，变换会将整个空间压扁到一个更低的维度。

我们以矩阵 $C = \begin{pmatrix} 1 & 1 \\ 2 & 2 \end{pmatrix}$ 为例。

变换前： 两个基向量是 [1,0] 和 [0,1]。
变换后：
- 第一个基向量 [1,0] 被变换到了 [1,1]。
- 第二个基向量 [0,1] 被变换到了 [2,2]。
结果： 两个基向量被压扁到了同一条直线上（斜率为1的直线），原来的整个二维平面被压缩成了一条线。由于面积变成了 0，所以这个变换也是不可逆的。

行列式为0 也是线性相关的代数体现。如果一个矩阵的两列是线性相关的（例如，其中一列是另一列的倍数，向量方向相同），那么它的行列式就必须为 0。

三个定理

单位矩阵的行列式为 1： $det(I)=1$ 这就像为我们的“空间缩放”设定了一个基准。单位矩阵代表了“什么都不做”的变换，所以它的缩放因子自然是 1。
交换任意两列，行列式变号： 如果交换矩阵的任意两列，行列式的值会乘以 -1。

例如：$det(\begin{pmatrix} a & b \ c & d \end{pmatrix})=−det(\begin{pmatrix} c & d \ a & b \end{pmatrix}) $

这个规则直接解释了行列式的符号性质。如果变换后空间的朝向发生了改变（比如翻转），那么行列式的符号就会随之改变。
对每一列，行列式都具有线性性质： 这个公理可以分解为两个部分：
- 缩放性： 如果将某一列向量乘以一个常数 k，那么整个行列式的值也会乘以 k。
  
  $det(v1, kv2, v3) = k* det(v1, v2, v3)$
- 可加性： 如果某一列是两个向量的和，那么行列式可以分解为两个行列式的和。
  
  $det(v1, v2 + v3) = det(v1, v2) + det(v1, v3)$

三、矩阵的逆

逆矩阵的概念和普通数字的倒数很像。比如，数字 5 的倒数是 1/5，因为 5×(1/5)=1。

对于矩阵来说，如果有一个方阵 A，并且存在一个矩阵 B，使得 A 乘以 B 等于单位矩阵 I，那么 B 就是 A 的逆矩阵，通常记作 $A^{−1}$。

用公式表示就是：$A×A^{−1}=A^{−1}×A=I$

注意： 只有满足以下条件的矩阵才可能有逆矩阵：

它必须是方阵（行数和列数相等）。
它的行列式不为零。如果行列式为零，该矩阵是奇异矩阵，它没有逆。

求解方法

求解逆矩阵有多种方法，最直观和常见的是高斯-约旦消元法。

我们知道，通过下面的这几种变换，可以实现矩阵在空间中的基本几何变换（拉伸、压缩、反转等等）

将矩阵的任意两行互换位置
将某一行乘以一个非零常数
将某一行的倍数加到另一行上

这些变换一般称之为初等行变换。

那么，高斯-约旦消元法的核心，是增广矩阵和等效行变换，它的核心逻辑如下：

将矩阵 A 和单位矩阵 I 组合成增广矩阵 [A∣I]
对矩阵 A 和 I 同时进行多次初等行变换，目标是将矩阵 A 变成单位矩阵。
当变换结束时，矩阵 A 变换为单位矩阵，而原来的单位矩阵 I 则变换成了原矩阵的逆$A^{−1}$。

计算示例

下面先来一个例子，快速感受下这个过程。

我们以一个 2×2 矩阵为例来说明。

设待求逆的矩阵为： $$ A = \begin{bmatrix} 3 & 1 \ 4 & 2 \end{bmatrix} $$

构建增广矩阵 $[A|I]$，将矩阵 $A$ 和一个相同维度的单位矩阵 $I$ 拼接在一起。

\[[A | I] = \left[ \begin{array}{cc|cc} 3 & 1 & 1 & 0 \\ 4 & 2 & 0 & 1 \end{array} \right] \]
通过行变换将左侧 $A$ 变为单位矩阵

目标1：使左上角元素为 1。将第一行 ($R_1$) 乘以 $1/3$ ($R_1 \rightarrow \frac{1}{3}R_1$)：

\[\left[ \begin{array}{cc|cc} 1 & 1/3 & 1/3 & 0 \\ 4 & 2 & 0 & 1 \end{array} \right] \]

目标2：使第一列的其他元素为 0。将第一行乘以 -4，并加到第二行 ($R_2$) 上 ($R_2 \rightarrow R_2 – 4R_1$)：

\[\left[ \begin{array}{cc|cc} 1 & 1/3 & 1/3 & 0 \\ 0 & 2/3 & -4/3 & 1 \end{array} \right] \]

目标3：使对角线上的元素都为 1。将第二行 ($R_2$) 乘以 $3/2$ ($R_2 \rightarrow \frac{3}{2}R_2$)：

\[\left[ \begin{array}{cc|cc} 1 & 1/3 & 1/3 & 0 \\ 0 & 1 & -2 & 3/2 \end{array} \right] \]

目标4：使第二列的其他元素为 0。} 将第二行乘以 $-1/3$，并加到第一行 ($R_1$) 上 ($R_1 \rightarrow R_1 – \frac{1}{3}R_2$)：

\[\left[ \begin{array}{cc|cc} 1 & 0 & 1 & -1/2 \\ 0 & 1 & -2 & 3/2 \end{array} \right] \]
提取逆矩阵。此时，增广矩阵的左侧已经是单位矩阵 $I$。

右侧的矩阵就是 $A$ 的逆矩阵 $A^{-1}$。

\[A^{-1} = \begin{bmatrix} 1 & -1/2 \\ -2 & 3/2 \end{bmatrix} \]
验证结果

通过计算 $A \times A^{-1}$ 来验证结果：

\[\begin{bmatrix} 3 & 1 \\ 4 & 2 \end{bmatrix} \times \begin{bmatrix} 1 & -1/2 \\ -2 & 3/2 \end{bmatrix} \]

\[= \begin{bmatrix} (3\times1 + 1\times(-2)) & (3\times(-1/2) + 1\times(3/2)) \\ (4\times1 + 2\times(-2)) & (4\times(-1/2) + 2\times(3/2)) \end{bmatrix} \]

\[= \begin{bmatrix} (3 – 2) & (-3/2 + 3/2) \\ (4 – 4) & (-2 + 3) \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = I \]

计算结果是单位矩阵 $I$，验证了 $A^{-1}$ 是正确的。

行变换

这个过程看上去并不复杂，但如果要知道为什么它能成功，还需要了解初等行变换的意义。

初等行变换，相当于对矩阵应用了一次线性变换，也相当于对矩阵左乘了一个初等矩阵（Elementary Matrix），初等矩阵的意思，就是由单位矩阵经过一次初等行变换（或初等列变换）得到的矩阵。

例如，将单位矩阵 I 变化，将第一行和第二行交换

\[I=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}, I_1 = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \]

那么，在计算左乘积时会有这样的特点：

\[I×A=A, \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} × \begin{bmatrix} 3 & 1 \\ 4 & 2 \end{bmatrix} = \begin{bmatrix} 3 & 1 \\ 4 & 2 \end{bmatrix} \]

\[I_1×A=A_1, \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} × \begin{bmatrix} 3 & 1 \\ 4 & 2 \end{bmatrix} = \begin{bmatrix} 4 & 2 \\ 3 & 1 \end{bmatrix} \]

可以看到，$I_1 $是 $I$ 应用了行交换的结果，而$A_1 $也是 $A$ 应用了行交换的结果。为什么是左乘积？是因为矩阵乘积的计算，是由左边矩阵的行与右边矩阵的列进行点积计算而来，当右边矩阵不变，左边矩阵的行进行初等变换（交换、缩放等）时，结果行也发生了相同的变换（交换、缩放等）。

所以，如果我们将矩阵求逆的计算理解为拆分变换的过程，就有：

对矩阵 $A$ 的多次变换理解为经过多个初等矩阵左乘的过程：

$(E_k⋯E_2E_1)A$

那么求逆的过程就是：

$(E_k⋯E_2E_1)[A∣I]=[(E_k⋯E_2E_1)A∣(E_k⋯E_2E_1)I]=[I ∣(E_k⋯E_2E_1)I ]$

这个过程相当于对 A 和 I 都应用同等过程的行变换 Ek..E1

其中，由于 $(E_k⋯E_2E_1)A=I$，那么说明：

$ A^{-1} = (E_k⋯E_2E_1) = (E_k⋯E_2E_1)I$

因此可以推导出，右边单位矩阵的变换结果就是矩阵的逆。

应用案例

在数学和工程领域，可以结合矩阵求逆的过程来求解线性方程组。

考虑一个如下的线性方程组：

\[\begin{cases} 2x + 3y = 8 \\ x – 2y = -3 \end{cases} \]

我们可以将其表示为矩阵形式 $A\vec{x} = \vec{b}$：

\[\begin{bmatrix} 2 & 3 \\ 1 & -2 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 8 \\ -3 \end{bmatrix} \]

其中，$A = \begin{bmatrix} 2 & 3 \\ 1 & -2 \end{bmatrix}$ 是系数矩阵，$\vec{x} = \begin{bmatrix} x \\ y \end{bmatrix}$ 是变量向量，$\vec{b} = \begin{bmatrix} 8 \\ -3 \end{bmatrix}$ 是常数向量。

求解 $\vec{x}$ 的一个方法是找到 $A$ 的逆矩阵 $A^{-1}$，然后计算 $\vec{x} = A^{-1}\vec{b}$。
我们将系数矩阵 $A$ 和一个相同维度的单位矩阵 $I$ 拼接在一起，形成增广矩阵 $[A | I]$：

\[[A | I] = \left[ \begin{array}{cc|cc} 2 & 3 & 1 & 0 \\ 1 & -2 & 0 & 1 \end{array} \right] \]

接下来通过行变换将左边的 $A$ 变成单位矩阵 $I$。具体变换过程如下：

交换第一行和第二行

\[\left[ \begin{array}{cc|cc} 1 & -2 & 0 & 1 \\ 2 & 3 & 1 & 0 \end{array} \right] \]

使第一列的其余元素变为 0，将第一行乘以 -2，并加到第二行上

\[\left[ \begin{array}{cc|cc} 1 & -2 & 0 & 1 \\ 0 & 7 & 1 & -2 \end{array} \right] \]

使对角线上的元素都变为 1，将第二行乘以 $1/7$

\[\left[ \begin{array}{cc|cc} 1 & -2 & 0 & 1 \\ 0 & 1 & 1/7 & -2/7 \end{array} \right] \]

使第二列的其余元素变为 0，将第二行乘以 2，并加到第一行上

\[\left[ \begin{array}{cc|cc} 1 & 0 & 2/7 & 3/7 \\ 0 & 1 & 1/7 & -2/7 \end{array} \right] \]

结果：获取逆矩阵和方程解

\[A^{-1} = \begin{bmatrix} 2/7 & 3/7 \\ 1/7 & -2/7 \end{bmatrix} \]

接下来，求解方程组 $\vec{x} = A^{-1}\vec{b}$：

\[\begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 2/7 & 3/7 \\ 1/7 & -2/7 \end{bmatrix} \begin{bmatrix} 8 \\ -3 \end{bmatrix} = \begin{bmatrix} (2/7)\times8 + (3/7)\times(-3) \\ (1/7)\times8 + (-2/7)\times(-3) \end{bmatrix} = \begin{bmatrix} (16-9)/7 \\ (8+6)/7 \end{bmatrix} = \begin{bmatrix} 7/7 \\ 14/7 \end{bmatrix} = \begin{bmatrix} 1 \\ 2 \end{bmatrix} \]

因此，方程组的解是 $x=1, y=2$。

在经典的最小二乘法线性回归算法中，矩阵求逆是一个重要过程。

四、小试牛刀

下面使用 numpy 来实现本文提到关于矩阵的计算过程，包括：行列式求解和矩阵求逆。

代码示例

import numpy as np

# 二阶矩阵
matrix_2x2_pos = np.array([[4, 2], [3, 1]])   # 行列式 > 0
matrix_2x2_zero = np.array([[1, 2], [2, 4]])  # 行列式 = 0
matrix_2x2_neg = np.array([[1, 2], [3, 4]])   # 行列式 < 0

# 三阶矩阵
matrix_3x3_pos = np.array([[2, 0, 1], [1, 1, 0], [3, 2, 1]])   # 行列式 > 0
matrix_3x3_zero = np.array([[1, 2, 3], [2, 4, 6], [3, 6, 9]])  # 行列式 = 0
matrix_3x3_neg = np.array([[0, 2, 1], [1, 0, 3], [4, 1, 2]])   # 行列式 < 0

# 求行列式
def print_determinant(matrix):
    det = np.linalg.det(matrix)
    print(f"矩阵:\n{matrix}")
    print(f"行列式: {det:.2f}")
    if det > 0:
        print("行列式为正数\n")
    elif det < 0:
        print("行列式为负数\n")
    else:
        print("行列式为零\n")

# 求逆
def inverse_matrix(matrix):
    det = np.linalg.det(matrix)
    print(f"矩阵:\n{matrix}")
    print(f"行列式: {det:.2f}")
    if det == 0:
        print(" 此矩阵不可逆（行列式为零）\n")
    else:
        inv = np.linalg.inv(matrix)
        print(" 矩阵的逆为：")
        print(inv, "\n")

# 输出所有行列式情况
print(" 二阶矩阵行列式")
print_determinant(matrix_2x2_pos)
print_determinant(matrix_2x2_zero)
print_determinant(matrix_2x2_neg)

print(" 三阶矩阵行列式")
print_determinant(matrix_3x3_pos)
print_determinant(matrix_3x3_zero)
print_determinant(matrix_3x3_neg)


# 求逆成功
print(" 求逆成功示例")
inverse_matrix(matrix_3x3_pos)

# 求逆失败
print(" 求逆失败示例")
inverse_matrix(matrix_3x3_zero)

执行上述程序，输出结果如下：

 二阶矩阵行列式
矩阵:
[[4 2]
 [3 1]]
行列式: -2.00
行列式为负数

矩阵:
[[1 2]
 [2 4]]
行列式: 0.00
行列式为零

矩阵:
[[1 2]
 [3 4]]
行列式: -2.00
行列式为负数

 三阶矩阵行列式
矩阵:
[[2 0 1]
 [1 1 0]
 [3 2 1]]
行列式: 1.00
行列式为正数

矩阵:
[[1 2 3]
 [2 4 6]
 [3 6 9]]
行列式: 0.00
行列式为零

矩阵:
[[0 2 1]
 [1 0 3]
 [4 1 2]]
行列式: 21.00
行列式为正数

 求逆成功示例
矩阵:
[[2 0 1]
 [1 1 0]
 [3 2 1]]
行列式: 1.00
 矩阵的逆为：
[[ 1.  2. -1.]
 [-1. -1.  1.]
 [-1. -4.  2.]] 

 求逆失败示例
矩阵:
[[1 2 3]
 [2 4 6]
 [3 6 9]]
行列式: 0.00
 此矩阵不可逆（行列式为零）

五、小结

在程序员眼里，矩阵只是一个普通的二维数组，但矩阵的数学意义远大于此，矩阵的几何意义是线性代数的核心思想，这篇文章的目的，是通过一些浅显的讲解来描述两个关键概念：行列式和逆。

行列式有很广泛的数学应用范畴，它的三个基本规则完美地描述了矩阵线性变换的关键特征：基准（det(I)=1）、方向（交换变号） 和缩放（线性性）；矩阵的逆则描述了矩阵对空间变换的撤销操作，通过矩阵和矩阵的逆我们可以实现关于空间的任意变换。

2025年9月
一	二	三	四	五	六	日
« 8月
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30