《Spatio-Temporal Representation With Deep Neural Recurrent Network in MIMO CSI Feedback》文献阅读

​ 该文献的作者是天津大学的吴华明老师，在2020年5月发表于IEEE WIRELESS COMMUNICATIONS LETTERS。

​ 该文献提出了一种基于深度学习的压缩CSI方法，使用深度循环神经网络(RNN)来学习时间相关性，根据不同结构下解耦的时空特征表示设计了特征提取模块，并采用深度可分离卷积来恢复信道。

1 研究背景

​ 在频分双工(FDD)MIMO网络中，UE可以估计出下行CSI，然后将CSI反馈给BS对下一个信号进行预编码。上行CSI反馈则由于BS处有大量天线，导致CSI反馈计算复杂度巨大。因此需要降低CSI反馈的开销，最新研究表明，应用深度学习来解决无线通信中的CSI反馈问题可以得到优秀的性能。

​ 文章的主要贡献是在CsiNet、ConvLSTM和RecCsiNet的基础上，设计了一种编码解码网络，称为ConvlstmCsiNet。在编码器中，利用ConvLSTM提取特征，并且用P3D替换了ConvLSTM中的卷积层；随后使用RecCsiNet作为编码器的压缩和解码器的解压模块；最后，把RefineNet中的标准卷积用深度可分离卷积代替作为解码器的信道恢复模块。

2 CSI反馈系统

​ 考虑频分双工MIMO下行链路，在BS上有Nt根天线，在每个UE上有一根天线，在OFDM中有\(\tilde{N}_{\mathrm{c}}\)个子载波，第n个子载波的接收信号为：

\[y_n=\tilde{\mathbf{h}}_n^H \mathbf{v}_n x_n+z_n \]

\(\tilde{\mathbf{h}}_n \in \mathbb{C}^{N_{\mathrm{t}} \times 1}, \mathbf{v}_n \in \mathbb{C}^{N_{\mathrm{t}} \times 1}, x_n \in \mathbb{C} \text {, 和 } z_n \in \mathbb{C}\)分别表示瞬时信道向量、预编码向量、调制的发射信号和第n个子载波上的加性噪声。CSI矩阵可以表示为：

\[\tilde{\mathbf{H}}=\left[\tilde{\mathbf{h}}_1, \tilde{\mathbf{h}}_2, \ldots, \tilde{\mathbf{h}}_{\tilde{N}_c}\right] \in \mathbb{C}^{N_t \times \tilde{N}_c} \]

假设每个UE都可以获得\(\tilde{\mathbf{H}}\)的估计，然后进行两个预处理，再反馈给BS：

• 首先用二维离散傅里叶变换(\(DFT\))处理\(\tilde{\mathbf{H}}\)，把它转换到角延迟域。
• 在延迟域中，除前几列非零外大多数元素都是零，因此保留前\({N}_{\mathrm{c}}\)列，其余的列删除，新的CSI矩阵大小为\({\mathbf{H}} \in \mathbb{C}^{N_t \times {N}_c}\)。

​ 假设对于给定的OFDM系统及其相关的预编码向量，信道矩阵H保持固定。然而它是会根据状态空间模型随时间而变化的，第t时步的瞬时CSI矩阵为\({H}_{t}=\left[\mathbf{h}_{1, t}, \mathbf{h}_{2, t}, \ldots, \mathbf{h}_{N_c, t}\right] \in \mathbb{C}^{N_t \times N_c}\),则下一时步的CSI矩阵表示为：

\[\mathbf{H}_{t+1}=\mathbf{F} \cdot \mathbf{H}_t+\mathbf{G} \cdot \mathbf{u}_t \]

其中\(\mathbf{u}_t \in \mathbb{C}^{N_t \times N_c},\mathbf{F}, \mathbf{G} \in \mathbb{C}^{N_t \times N_t}\)分别代表加性噪声和权重方阵，\(u_t^{(i, j)} \sim N\left(0, \sigma_u^2\right)\)。用\(α\)来表示相邻CSI矩阵之间的相关性，可令\(F = (1 – α^2)I,G = {α^2}I\)。所以在时间T内随时间变换的CSI矩阵可表示为\(\left\{\mathbf{H}_t\right\}_{t=1}^{T}=\left\{\mathbf{H}_1, \mathbf{H}_2, \ldots, \mathbf{H}_T\right\}\)。

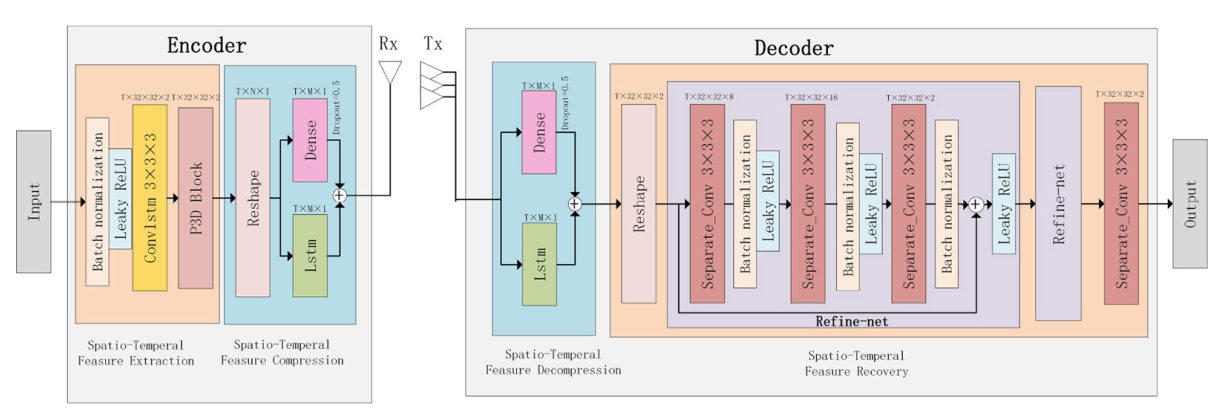
​ 如图1所示，在CSI反馈的过程中，首先将\(\left\{\mathbf{H}_t\right\}_{t=1}^{T}\)分为实部和虚部，矩阵中的所有元素都转化为实数，并在\([0,1]\)内归一化。随后利用DFT变换和截断操作将反馈参数个数降低为\(N= 2*N_c*N_t\)，这在MIMO中仍然是非常大的。因此需要输入编码器进行特征提取和压缩，得到M维的码字，压缩率为\(γ=M/N\)。码字作为BS中解码器的输入，经过解压缩和特征恢复得到\(\widehat{{\mathbf{H}}}_t\)，最后通过逆\(DFT\)和补0操作得到\(\widehat{\tilde{\mathbf{H}}}_t\)。

​ 图1中，不同的网络层有不同的颜色，每层上方是输出的形状，用\(T × H × W × C\)或者\(T × L × C\)表示，\(T,H,W,C\)和\(L\)分别表示循环神经网络的时间步，特征图的高度，特征图的宽度，通道数和码字长度。

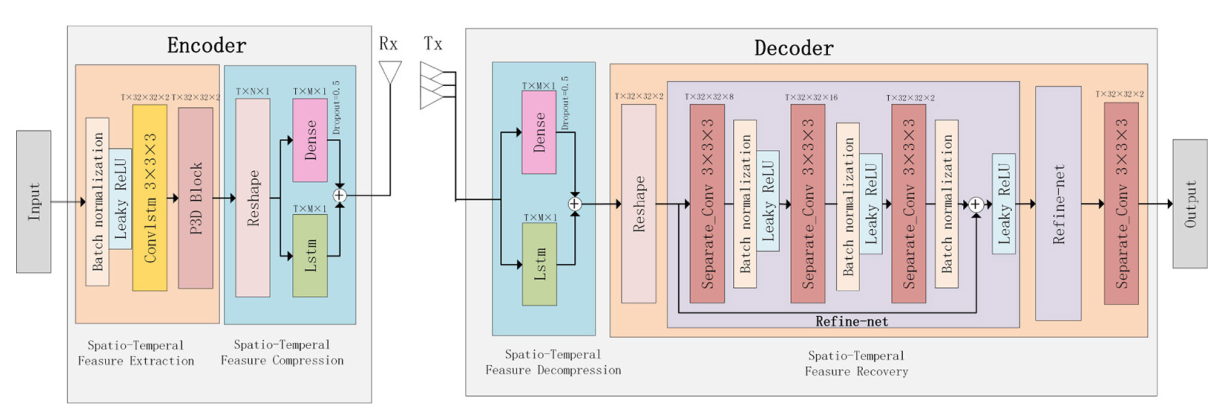
图1 ConvlstmCsiNet

3 ConvlstmCsiNet With P3D Blocks

3.1 ConvlstmCsiNet

3.1.1 特征提取

​ 在图2 CsiNet的基础上改进了特征提取模块，在卷积层前增加了卷积长短期记忆(ConvLSTM)层，从之前时间步长的输入中学习时间相关性，压缩时间冗余，它可以帮助卷积在特征提取中捕获更多有用的时间信息。

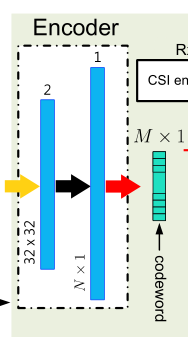
图2 CsiNet的编码器

​ ConvLSTM是为了解决随计算时间增加时间序列梯度消失的问题。与LSTM相比，主要的变化是将权值的计算由线性运算转换为卷积运算，不仅能捕获时间相关性，还能同时获得图像特征中的详细局部信息。如图3所示，它通过三个遗忘门、输入门和输出门，包括sigmoid激活层、tanh激活层和卷积运算，就能够对状态信息进行删除或添加。此外，由于卷积运算比线性运算需要的参数少得多，ConvLSTM可以帮助减小网络参数的大小。

图3 ConvLSTM

3.1.2 特征压缩和解压

​ 参考RecCsiNet的压缩解压模块，通过并联全连接层和LSTM，把N长的向量压缩成M长的码字，如图4所示。这里并没有完全用ConvLSTM代替LSTM，因为LSTM在权值计算中进行FC运算，在整体信息交互方面表现更好，更适合于特征压缩，而ConvLSTM更适合于描述局部详细信息。

图4 RecCsiNet的压缩解压模块

3.1.3 特征恢复

​ 采用CsiNet的RefineNet作为基本结构。每个RefineNet块有3个串联的卷积层，分别输出8、16和2个特征图。特征恢复模块使用两个RefineNet块对H的初步粗略估计进行了细化，CsiNet中的结果证明两个块足以恢复CSI矩阵，更多块将导致参数冗余，如图5所示。在两个RefineNet之后，还有一个卷积层和一个sigmoid激活层，它输出恢复H的实部和虚部最终结果。

图5 CsiNet的解码器

​ 在RefineNet的基础上，用深度可分离卷积（depthwise separable convolution，DS-Conv）代替其中的所有卷积层，不仅减少了参数的数量，而且还让RefineNet实现更好的性能和更高的恢复精度。DS-Conv分为两个步骤，深度卷积如图6所示，点卷积如图7所示。

深度卷积是一组卷积，每个卷积分别负责一个特征图，因此有M个3 × 3 × 3个深度为1的深度卷积滤波器，输出M个特征图。

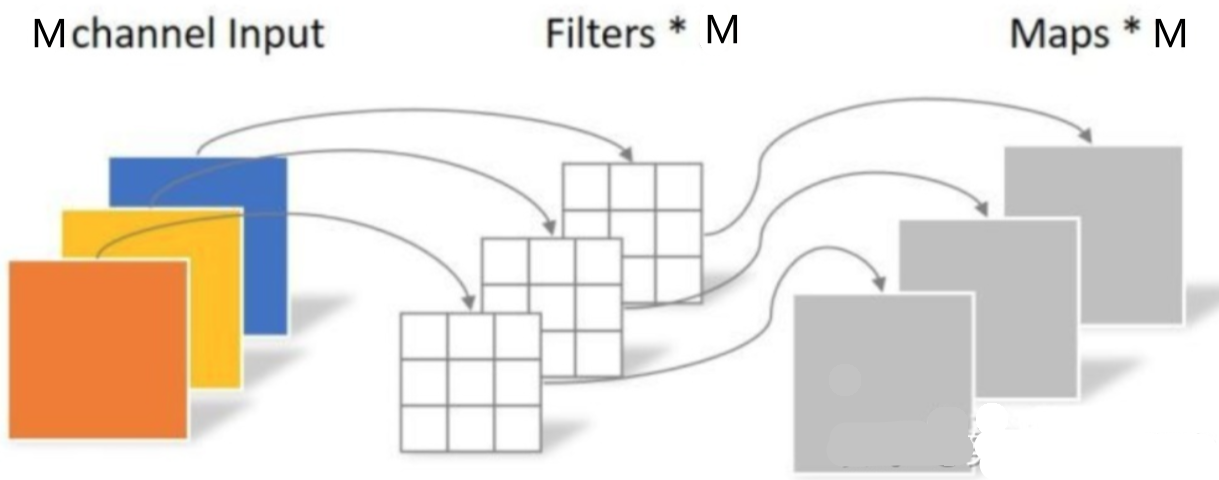
图6 深度卷积

点卷积是N个1 × 1 × 1的深度为M的卷积，处理深度卷积得到的M个特征图，输出N个特征图。

图7 点卷积

深度卷积主要是获取每个信道的特征，点卷积是获取上行信道和下行信道的维度，以及信道之间的信息整合和交互，有助于卷积更好地理解不同信道之间的相关性。DS-Conv3D也可以在一定程度上减小特征恢复模块的参数大小，此外由于大量使用了点卷积，一些高度优化矩阵乘法如GEMM可以直接完成，而不需要im2col的预处理操作，大大提高了运算效率。

3.2 ConvlstmCsiNet的解耦时空特征提取

​ 为了进一步完善ConvlstmCsiNet，还重点研究了特征提取模块中的时空特征表示。ConvLSTM首先提取单元格中的空间特征，然后对单元格进行循环，形成时间序列，这表明提取空间特征和时间特征具有一定的独立性。

​ 因此，可以用Pseudo-3D (P3D)替换掉特征提取模块中的卷积层。P3D的结构如图8所示，它的关键思想是分别在时间域和空间域捕获特征。假设我们有尺寸为\(Td × Sd × Sd\)的三维卷积滤波器(\(Td\)和\(Sd\)分别表示时间深度和空间深度)，它们可以自然解耦为空间域上的\(1 × Sd × Sd\)卷积滤波器和时间域上的\(Td × 1 × 1\)卷积滤波器。P3D以串联或并联的方式用两个滤波器取代标准卷积层，这样既可以减少参数的数量，又可以降低计算复杂度。在图8中提出了3种组合结构，还使用了ResNet的跳跃连接方法，它可以直接将数据流传递到后续层，导致模型退化为浅网络，从而通过跳过那些不必要的层来简化优化，提高神经网络的鲁棒性。

图8 P3D

基于ConvlstmCsiNet，将P3D-A, P3D-B和P3D-C块分别替代特征提取模块中的卷积层，分别称为ConvlstmCsiNet- A, ConvlstmCsiNet- B和ConvlstmCsiNet- C。

4 实验结果

​ 通过COST 2100信道模型创建了两种信道矩阵：1）5.3GHz室内场景；2）300MHz农村室外场景。BS位于室内和室外场景中长度分别为20m和400m的正方形区域的中心，而UE则随机位于每个样本的正方形区域。基站天线阵列数量为32，子载波数为1024，将信道矩阵转换到角延迟域时，保留信道矩阵的前32行，即H的大小为32 × 32。根据公式(3)，在每个时间步长之间加入微小的高斯白噪声\(σ_u = 10^{−3}\)和相邻信道的相关系数\(α\)，将二维CSI矩阵扩展为T时间序列的时变CSI矩阵，其中T为循环时间步长，为方便设置为4。训练集、验证集和测试集分别包含100000、30000和20000个样本。前1000个epoch的学习率为\(10^{−3}\)，1000 ~ 1200个epoch的学习率为\(5 × 10^{−4}\)，最后1200 ~ 1500个epoch的学习率为\(10^{−4}\)。引用两个指标来衡量网络性能的优劣：

• 归一化均方误差 (NMSE)，它能够量化输入\(\left\{\mathbf{H}_t\right\}_{t=1}^{T}\)和输出\(\left\{\hat{\mathbf{H}}_t\right\}_{t=1}^T\)，定义为：

\[\mathrm{NMSE}=\mathbb{E}\left\{\frac{1}{T} \sum_{t=1}^T \frac{\left\|\mathbf{H}_t-\hat{\mathbf{H}}_t\right\|_F^2}{\left\|\mathbf{H}_t\right\|_F^2}\right\} \]

• 余弦相似度\(ρ\)，它能够描述了原始CSI矩阵\(\tilde{\mathbf{H}}\)和恢复的\(\widehat{\tilde{\mathbf{H}}}\)之间的相似性，定义为：

\[\rho=\mathbb{E}\left\{\frac{1}{T} \frac{1}{\tilde{N}_c} \sum_{t=1}^T \sum_{n=1}^{\tilde{N}_c} \frac{\left|\hat{\tilde{\mathbf{h}}}_{n, t}^H \cdot \tilde{\mathbf{h}}_{n, t}\right|}{\left\|\hat{\tilde{\mathbf{h}}}_{n, t}\right\|_2\left\|\tilde{\mathbf{h}}_{n, t}\right\|_2}\right\} \]

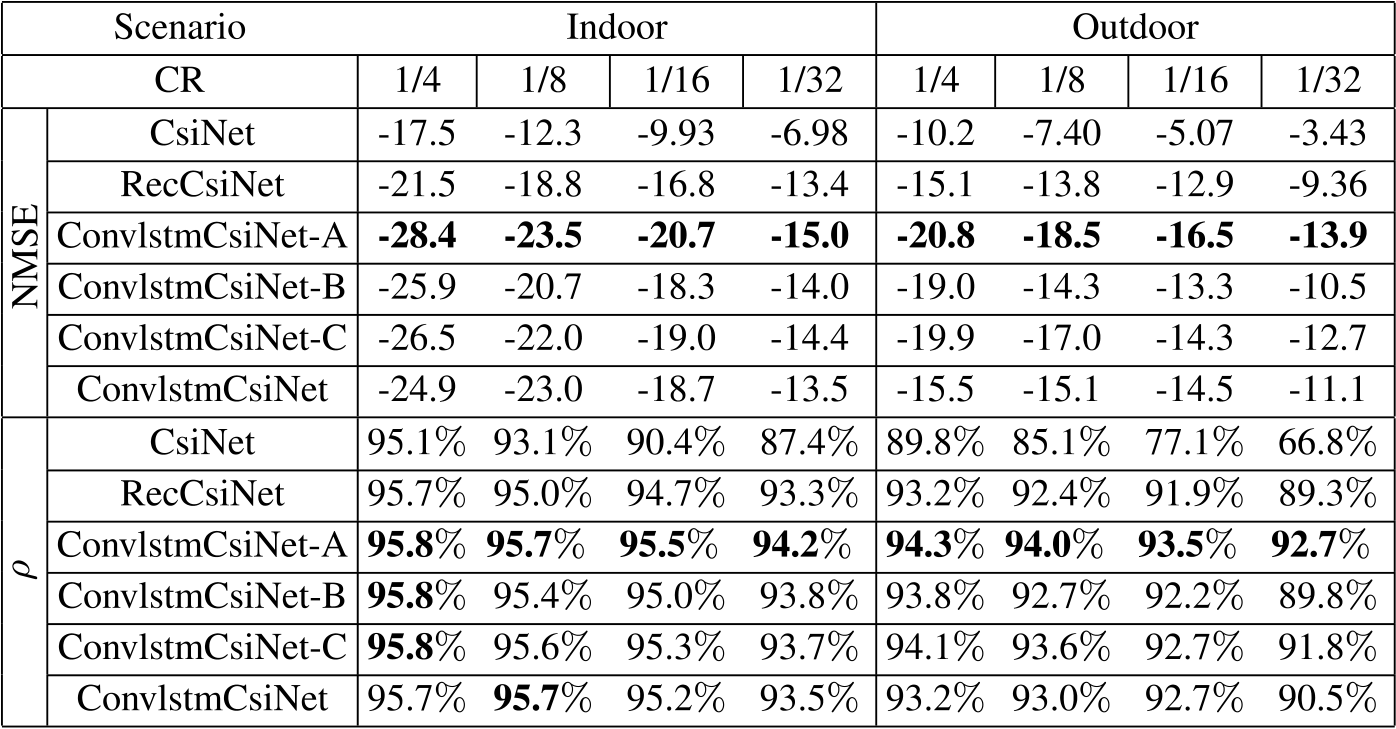
将本文的方法与基于深度学习的方法如CsiNet和RecCsiNet进行比较，对应的NMSE和\(ρ\)如表1所示，其中最好的结果用粗体标记。由于NMSE的值太小，所以用\(log(NMSE)\)来表示。

​ 结果表明，四种提出网络的性能都优于CsiNet和RecCsiNet，在带P3D的网络中，ConvlstmCsiNet-A的性能最好，而ConvlstmCsiNet-B的性能最差，说明串联比并联方式的时空滤波器性能更好。在室外条件下，四种模型在室外场景下都比在室内场景下获得了更高的性能提升，表明它们具有较高的鲁棒性，与ConvlstmCsiNet相比，使用P3D的网络获得了更好的性能，说明P3D对提高模型的鲁棒性有积极的作用。

表1 α=0.1时不同压缩率下的NMSE和ρ

5 结论

​ 在特征提取和恢复模块中分别采用RNN和深度可分离卷积，提出了一种新的CSI反馈网络结构。实验结果表明，该网络的鲁棒性、准确性和质量都比CsiNet和RecCsiNet要强。

6 学习收获

文章的主要工作如下：

1. ConvLSTM提取信道；
2. P3D优化ConvLSTM；
3. RecCsiNet压缩和解压；
4. RefineNet恢复信道；
5. DS-Conv优化RefineNet。

它是在CsiNet和RecCsiNet的基础上，加入了ConvLSTM、P3D和DS-Conv，从实验结果来看表现的性能非常优秀。这篇文献在一些细节参数上讲的比以前看过的文章清楚，通过阅读这篇文献，我新学习了ConvLSTM、P3D和DS-Conv网络模型，了解了它们的一些特点和用处，也让我想去阅读更多相关文献来看是否还有其它的优化方法。