3 列表和元组

主要内容：

• 列表和元组有什么用？
• 在列表/元组中查找的复杂性是什么？
• 如何实现这种复杂性？
• 列表和元组有哪些区别？
• 如何对列表进行追加？
• 什么时候应该使用列表和元组？

编写高效程序最重要的一点是了解所使用数据结构的保证。事实上，高效编程的很大一部分就是要知道你想对数据提出什么问题，并选择一种能快速回答这些问题的数据结构。在本章中，我们将讨论列表和元组可以快速回答哪些类型的问题，以及它们是如何做到这一点的。

列表和元组是一类名为数组的数据结构。数组是具有某种内在排序的扁平数据列表。通常在这类数据结构中，元素的相对排序和元素本身一样重要！此外，这种对排序的先验知识非常有价值：通过知道数组中的数据位于特定位置，我们可以在 O(1) 的时间内检索到这些数据！实现数组的方法也有很多种，每种方案都有其有用的特性和保证。这就是为什么在 Python 中我们有两种数组类型：列表和元组。列表是动态数组，允许我们修改和调整存储数据的大小，而元组是静态数组，其内容是固定不变的。

让我们来解读一下前面的表述。计算机上的系统内存可以看作是一系列编号的桶，每个桶都可以存储一个数字。Python 通过引用将数据存储在这些桶中，这意味着数字本身只是指向或引用我们实际关心的数据。因此，这些桶可以存储我们想要的任何类型的数据（而 numpy 数组则不同，它有一个静态类型，只能存储该类型的数据）。

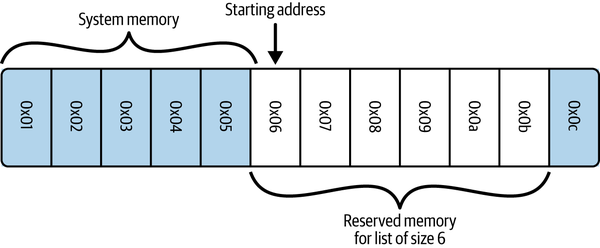
当我们要创建数组（以及列表或元组）时，首先必须分配一个系统内存块（该内存块的每一部分都将用作实际数据的整数大小指针）。这需要进入系统内核，请求使用 N 个连续的内存桶。下图显示了大小为 6 的数组（本例中为列表）的系统内存布局示例。

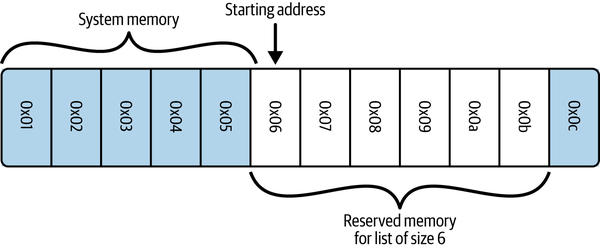
注意：在 Python 中，列表也存储它们的大小，因此在分配的六个块中，只有五个是可用的–第三个元素是长度。

为了查找列表中的任何特定元素，我们只需知道我们想要的元素，并记住我们的数据是从哪个存储桶开始的。由于所有数据将占用相同的空间（一个 “桶”，或者更具体地说，一个指向实际数据的整数大小的指针），因此我们不需要知道存储的数据类型来进行计算。

如果你知道由 N 个元素组成的列表在内存中的起始位置，你将如何在列表中查找任意元素？
例如，如果我们需要检索数组中的第零个元素，我们只需转到序列中的第一个存储桶 M，然后读出其中的值。另一方面，如果我们需要数组中的第五个元素，我们就会转到位于 M + 5 位置的桶，然后读取其中的内容。因此，通过将数据存储在连续的存储桶中，并了解数据的排序，无论数组有多大，我们都可以通过一步（或 O(1)）就知道要查看哪个存储桶来定位数据（例 3-1）。

例 3-1. 不同大小列表中的查找计时

>>> %%timeit l = list(range(10))
        ...: l[5]
        ...:
14 ns ± 0.182 ns per loop (mean ± std. dev. of 7 runs, 100,000,000 loops each)

>>> %%timeit l = list(range(10_000_000))
        ...: l[100_000]
        ...:
13.9 ns ± 0.123 ns per loop (mean ± std. dev. of 7 runs, 100,000,000 loops each)

如果给我们一个顺序未知的数组，并希望检索某个特定元素，该怎么办？如果排序已知，我们只需查找该特定值即可。但在这种情况下，我们必须进行搜索操作。解决这个问题的最基本方法是线性搜索，我们遍历数组中的每个元素，检查它是否是我们想要的值，如例 3-2 所示。

例 3-2. 对列表进行线性搜索

import timeit


def linear_search(needle, array):
    for i, item in enumerate(array):
        if item == needle:
            return i
    return -1


if __name__ == "__main__":
    setup = "from __main__ import (linear_search, haystack, needle)"
    iterations = 1000

    for haystack_size in (10000, 100000, 1000000):
        haystack = range(haystack_size)
        for needle in (1, 6000, 9000, 1000000):
            index = linear_search(needle, haystack)
            t = timeit.timeit(
                stmt="linear_search(needle, haystack)", setup=setup, number=iterations
            )
            print(
                f"Value {needle: <8} found in haystack of "
                f"size {len(haystack): <8} at index "
                f"{index: <8} in {t/iterations:.5e} seconds"
            )

执行结果：

# python linear_search.py
Value 1        found in haystack of size 10000    at index 1        in 1.32893e-07 seconds
Value 6000     found in haystack of size 10000    at index 6000     in 2.02747e-04 seconds
Value 9000     found in haystack of size 10000    at index 9000     in 3.04364e-04 seconds
Value 1000000  found in haystack of size 10000    at index -1       in 3.49609e-04 seconds
Value 1        found in haystack of size 100000   at index 1        in 1.31818e-07 seconds
Value 6000     found in haystack of size 100000   at index 6000     in 2.06552e-04 seconds
Value 9000     found in haystack of size 100000   at index 9000     in 3.20001e-04 seconds
Value 1000000  found in haystack of size 100000   at index -1       in 3.51215e-03 seconds
Value 1        found in haystack of size 1000000  at index 1        in 1.31243e-07 seconds
Value 6000     found in haystack of size 1000000  at index 6000     in 1.98086e-04 seconds
Value 9000     found in haystack of size 1000000  at index 9000     in 3.07604e-04 seconds
Value 1000000  found in haystack of size 1000000  at index -1       in 3.37868e-02 seconds

这种算法的最差性能为 O(n)。当我们搜索不在数组中的元素时，就会出现这种情况。为了知道我们要搜索的元素不在数组中，我们必须先将它与其他元素进行核对。最终，我们将得到最后的 return -1 语句。事实上，这种算法正是 list.index()所使用的算法。

要想提高速度，唯一的办法就是了解数据在内存中的放置方式，或者我们所持有的数据桶的排列方式。例如，哈希表（“字典和集合是如何工作的？”）是字典和集合的基本数据结构，它通过在插入/检索时增加额外开销并强制对项目进行严格而特殊的排序，以 O(1) 的速度解决了这个问题。另外，如果对数据进行排序，使每个条目都比左边（或右边）的相邻条目大（或小），那么就可以使用专门的搜索算法，将查找时间降低到 O(log n)。然而，有时使用这些搜索算法是最好的解决方案（尤其是搜索算法非常灵活，允许你以创造性的方式定义搜索）。

• 练习
  给定以下数据，编写一个算法来查找值 61 的索引：[9, 18, 18, 19, 29, 42, 56, 61, 88, 95]
  既然知道数据是有序的，怎样才能更快地完成这项工作？
  提示：如果将数组一分为二，就可以知道左边的所有值都小于右边集合中最小的元素。你可以使用这个方法！

3.1 更高效的搜索

如前所述，如果我们先对数据进行排序，使某一项左边的所有元素都比该项小（或大），我们就能获得更好的搜索性能。比较是通过对象的 eq 和 lt 神奇函数完成的，如果使用自定义对象，也可以由用户自定义。

如果没有 eq 和 lt 方法，自定义对象将只与相同类型的对象进行比较，比较将使用实例在内存中的位置进行。定义了这两个神奇的函数后，你就可以使用标准库中的 functools.total_orderingdecorator 自动定义所有其他排序函数，尽管在性能上会有一点损失。

必要的两个要素是排序算法和搜索算法。Python 列表有一个使用 Tim 排序的内置排序算法。在最佳情况下，Tim 排序能以 O(n) 的速度对列表进行排序（在最差情况下，排序速度为 O(n log n)）。它通过利用多种类型的排序算法，并使用启发式方法来猜测哪种算法在给定数据的情况下性能最佳，从而实现这一性能（更具体地说，它混合了插入和合并排序算法）。

对列表进行排序后，我们可以使用二进制搜索（例 3-3）找到所需的元素，其平均复杂度为 O（log n）。它首先查看列表的中点，然后将该值与所需值进行比较。如果这个中点的值小于我们的期望值，我们就会考虑列表的右半部分，然后像这样继续将列表减半，直到找到该值，或者已知该值不会出现在排序列表中。因此，我们不需要像线性搜索那样读取列表中的所有值，而只需要读取其中的一小部分。

例 3-3. 高效搜索排序列表–二进制搜索

import timeit


def binary_search(needle, haystack):
    # imin and imax store the bounds of the haystack that we are currently
    # considering.  This starts as the bounds of the haystack and slowly
    # converges to surround the needle.
    imin, imax = 0, len(haystack)
    while True:
        if imin >= imax:
            return -1
        midpoint = (imin + imax) // 2
        if haystack[midpoint] > needle:
            imax = midpoint
        elif haystack[midpoint] < needle:
            imin = midpoint + 1
        else:
            return midpoint


if __name__ == "__main__":
    setup = "from __main__ import (binary_search, haystack, needle)"
    iterations = 10000

    for haystack_size in (10000, 100000, 1000000):
        haystack = range(haystack_size)
        for needle in (1, 6000, 9000, 1000000):
            index = binary_search(needle, haystack)
            t = timeit.timeit(
                stmt="binary_search(needle, haystack)", setup=setup, number=iterations
            )
            print(
                f"Value {needle: <8} found in haystack of "
                f"size {len(haystack): <8} at index "
                f"{index: <8} in {t/iterations:.5e} seconds"
            )

执行结果：

# python binary_search.py
Value 1        found in haystack of size 10000    at index 1        in 9.15618e-07 seconds
Value 6000     found in haystack of size 10000    at index 6000     in 1.24657e-06 seconds
Value 9000     found in haystack of size 10000    at index 9000     in 1.21479e-06 seconds
Value 1000000  found in haystack of size 10000    at index -1       in 1.66498e-06 seconds
Value 1        found in haystack of size 100000   at index 1        in 1.15999e-06 seconds
Value 6000     found in haystack of size 100000   at index 6000     in 1.76719e-06 seconds
Value 9000     found in haystack of size 100000   at index 9000     in 1.57295e-06 seconds
Value 1000000  found in haystack of size 100000   at index -1       in 2.03157e-06 seconds
Value 1        found in haystack of size 1000000  at index 1        in 1.36514e-06 seconds
Value 6000     found in haystack of size 1000000  at index 6000     in 1.74420e-06 seconds
Value 9000     found in haystack of size 1000000  at index 9000     in 1.96218e-06 seconds
Value 1000000  found in haystack of size 1000000  at index -1       in 2.39626e-06 seconds

通过这种方法，我们可以查找列表中的元素，而无需使用字典这种潜在的重型解决方案。尤其是当操作的数据列表本质上是排序的时候。在列表中进行二进制搜索以查找对象比首先将数据转换为字典，然后对其进行单次查找更有效。虽然字典查找只需 O(1)，但将数据转换为字典却需要 O(n)（而且字典没有重复键的限制可能并不可取）。另一方面，二进制搜索需要 O(log n)。

此外，Python 标准库中的 bisect 模块简化了这一过程，除了使用经过大量优化的二进制搜索查找元素外，还提供了在保持列表排序的同时向列表中添加元素的简便方法。它通过提供替代函数，将元素添加到正确的排序位置。由于列表始终保持排序，我们可以很容易地找到我们要找的元素（相关示例可在 bisect 模块的文档中找到）。此外，我们还可以使用 bisect 快速找到最接近的元素（例 3-4）。这对于比较两个相似但不完全相同的数据集非常有用。

• 例 3-4. 使用 bisect 模块查找列表中的近似值

import bisect
import random


def find_closest(haystack, needle):
    # bisect.bisect_left will return the first value in the haystack
    # that is greater than the needle
    i = bisect.bisect_left(haystack, needle)
    if i == len(haystack):
        return i - 1
    elif haystack[i] == needle:
        return i
    elif i > 0:
        j = i - 1
        # since we know the value is larger than needle (and vice versa for the
        # value at j), we don't need to use absolute values here
        if haystack[i] - needle > needle - haystack[j]:
            return j
    return i


if __name__ == "__main__":
    important_numbers = []
    for i in range(10):
        new_number = random.randint(0, 1000)
        bisect.insort(important_numbers, new_number)

    # important_numbers will already be in order because we inserted new elements
    # with bisect.insort
    print(important_numbers)
    # > [14, 265, 496, 661, 683, 734, 881, 892, 973, 992]

    closest_index = find_closest(important_numbers, -250)
    print(f"Closest value to -250: {important_numbers[closest_index]}")
    # > Closest value to -250: 14

    closest_index = find_closest(important_numbers, 500)
    print(f"Closest value to 500: {important_numbers[closest_index]}")
    # > Closest value to 500: 496

    closest_index = find_closest(important_numbers, 1100)
    print(f"Closest value to 1100: {important_numbers[closest_index]}")
    # > Closest value to 1100: 992

执行结果

[26, 69, 153, 159, 172, 221, 336, 426, 772, 859]
Closest value to -250: 26
Closest value to 500: 426
Closest value to 1100: 859

一般来说，这涉及到编写高效代码的基本规则：选择正确的数据结构并坚持使用！虽然可能有更高效的数据结构用于特定操作，但转换到这些数据结构的成本可能会抵消任何效率提升。

3.2 列表与元组

如果列表和元组都使用相同的底层数据结构，那么两者之间有什么区别呢？概括起来，主要区别如下：

• 列表是动态数组；它们是可变的，允许调整大小（改变所保存元素的数量）。
• 元组是静态数组；它们是不可变的，一旦创建了元组，它们所引用的数据就不会改变。
• Python 运行时会缓存元组，这意味着我们不需要每次使用元组时都与内核对话来预留内存。

这些差异概括了两者在哲学上的不同：元组用于描述一个不变事物的多个属性，而列表可以用来存储完全不同对象的数据集合。例如，电话号码的各个部分非常适合用元组来表示：它们不会发生变化，即使发生变化，它们也代表了一个新的对象或不同的电话号码。同样，多项式的系数也适合元组，因为不同的系数代表不同的多项式。另一方面，目前正在阅读这本书的人的姓名更适合列表：数据的内容和大小都在不断变化，但始终代表同一个概念。

值得注意的是，列表和元组都可以使用混合类型。正如你将看到的，这可能会带来相当大的开销，并减少一些潜在的优化。如果我们强制所有数据为同一类型，就可以消除这种开销。在第 6 章中，我们将讨论如何通过使用 numpy 来减少内存使用量和计算开销。此外，像标准库模块 array 这样的工具也可以在其他非数值情况下减少这些开销。这暗指了执行编程中的一个要点，我们将在后面的章节中谈到：通用代码要比专为解决特定问题而设计的代码慢得多。

此外，与可以调整大小和更改的列表相比，元组的不变性使其成为一种轻量级数据结构。这意味着在存储元组时，内存开销不大，对元组的操作也非常简单。而对于列表，正如你将学习到的，其可变性是以存储它们所需的额外内存和使用它们时所需的额外计算为代价的。

• 练习:对于下面的示例数据集，你会使用元组还是列表？为什么？
  • 前 20 个质数
  • 编程语言名称
  • 一个人的年龄、体重和身高
  • 一个人的生日和出生地
  • 某场台球比赛的结果
  • 一系列连续桌球比赛的结果
• 解决方案：
  • 元组，因为数据是静态的，不会改变。
  • 列表，因为数据集在不断增长。
  • 列表，因为值需要更新。
  • 元组，因为信息是静态的，不会改变。
  • 元组，因为数据是静态的。
  • 列表，因为会有更多的游戏进行。(事实上，我们可以使用元组列表，因为每场比赛的结果都不会改变，但随着比赛的增加，我们需要添加更多的结果）。

参考资料

• 软件测试精品书籍文档下载持续更新 https://github.com/china-testing/python-testing-examples 请点赞，谢谢！
• 本文涉及的python测试开发库 谢谢点赞！ https://github.com/china-testing/python_cn_resouce
• python精品书籍下载 https://github.com/china-testing/python_cn_resouce/blob/main/python_good_books.md
• Linux精品书籍下载 https://www.cnblogs.com/testing-/p/17438558.html
• python八字排盘 https://github.com/china-testing/bazi

3.2.1 动态数组：列表

创建列表后，我们可以根据需要自由更改其内容：

>>> numbers = [5, 8, 1, 3, 2, 6]
>>> numbers[2] = 2 * numbers[0]
>>> numbers
[5, 8, 10, 3, 2, 6]

如前所述，这一操作的运算量为 O(1)，因为我们可以立即找到存储在第 0 个和第 2 个元素中的数据。
此外，我们还可以在列表中添加新数据并增加其大小：

>>> len(numbers)
6
>>> numbers.append(42)
>>> numbers
[5, 8, 10, 3, 2, 6, 42]
>>> len(numbers)
7

之所以能做到这一点，是因为动态数组支持调整大小操作，从而增加数组的容量。当一个大小为 N 的 list 首次被追加时，Python 必须创建一个新的 list，这个新 list 的大小必须足以容纳原来的 N 个条目和被追加的额外条目。但是，为了给将来的追加提供额外的空间，实际上并不是分配 N + 1 个项，而是分配 M 个项（M > N）。然后将旧列表中的数据复制到新列表中，并销毁旧列表。
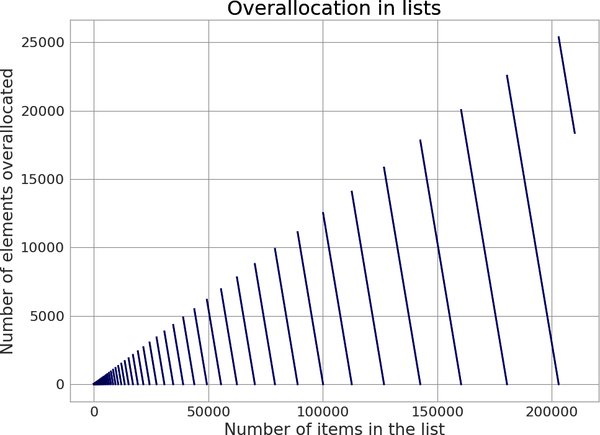
这样做的理念是，一次追加可能是多次追加的开始，通过申请额外空间，我们可以减少分配的总次数，从而减少所需的内存拷贝总数。这一点很重要，因为内存拷贝的成本可能会很高，尤其是当列表大小开始增大时。下图显示了 Python 3.12 中的这种总体分配。

• 例 3-5. Python 3.12 中的列表分配公式

M = (N + (N >> 3) + 6) & ~3

如果使用追加创建一个包含 1,000,000 个元素的 list，Python 将为 1,056,084 个元素分配空间，总计分配了 56,084 个元素！

因此，N 会随着我们添加新数据而增加，直到 N == M。此时，没有多余的空间插入新数据，我们必须创建一个有更多额外空间的新列表。根据例 3-5 中的等式，这个新列表有额外的空间，我们将旧数据复制到新空间。使用这种方法时，Python 通常会重新分配大约 12.5% 的列表空间，以减少列表追加的时间。然而，对于小的 list，这个比例可能会高得多–对于一个只有 1 个项的 list，需要分配 4 个项，而对于 9 个项的 list，则需要分配 16 个项！
下图直观地展示了这种复制、总体分配和追加的机制。图中显示了例 3-6 中对列表 l 执行的各种操作。

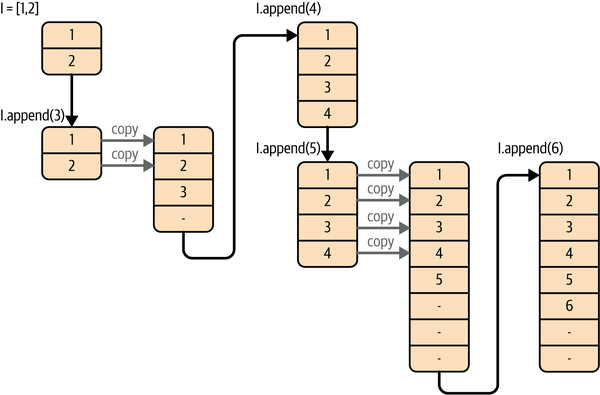
• 例 3-6. 调整列表大小

l = [1, 2]
for i in range(3, 7):
    l.append(i)

为了使潜在的静态列表保持较小的规模，只有在第一次追加时才会进行总体分配。在直接创建列表时，如上例，只分配所需的元素数。
虽然分配的额外余量通常很小，但也会增加。在例 3-7 中，我们可以看到，如果我们有许多小列表，每个列表都有开销，那么很快就会造成资源的大量使用。

• 例 3-7. 总体分配对内存的影响

import sys
import random


def total_size(obj):
    """
    Recursively calculates the total size of a Python object in memory,
    including its contents.

    Returns:
        int: The total size of the object in bytes.
    """
    children = 0
    try:
        children = sum(total_size(item) for item in obj)
    except TypeError:
        pass
    return sys.getsizeof(obj) + children


def sample_comp(a, b, N):
    return [random.randint(a, b) for _ in range(N)] 


def sample_list(a, b, N):
    return list([random.randint(a, b) for _ in range(N)])  

N_samples = 1_000_000
sample_size = 9
data_comp = [sample_comp(0, 100, sample_size) for _ in range(N_samples)]
data_list = [sample_list(0, 100, sample_size) for _ in range(N_samples)]

size_comp = max_size = total_size(data_comp) / 1e6
size_list = total_size(data_list) / 1e6

print(f"Creating {N_samples:,d} samples of {sample_size} items each")
print(f"Data Comprehension size: {size_comp:0.2f} Mb")
print(f"Data List size: {size_list:0.2f} Mb ({max_size/size_list:0.2f}x smaller)")

执行结果：

# python test.py
Creating 1,000,000 samples of 9 items each
Data Comprehension size: 444.45 Mb
Data List size: 396.45 Mb (1.12x smaller)

我们创建 N 个从 at 到 b 的随机整数。这个数据 “样本 ”可以是现实世界中的任何东西–用户点击的最后五个链接或某个目录中的文件名。不过，由于它是通过列表理解创建的，因此已经进行了总体分配。
在这里，我们的操作与之前的相同；不过，一旦数据创建完成，我们就将其传递给 list，以重新创建列表，但不进行任何总体分配。
我们可以从前面的示例中看到，重新分配开销的增加速度有多快。在这个相当常见的例子中，我们有许多小列表，内存增加了 1.12 倍，相当于浪费了 48 Mb 内存。在进行数据处理时，内存可能是最宝贵的资源，而这一简单的改变就能大大提高内存的整体使用率。我们很快就会看到如何通过元组将这一数字进一步降低（在第 12 章中，我们将进一步探讨这一主题）。

3.2.2 静态数组：元组

如果将其与列表中的追加操作相比较，我们会发现追加操作的速度为 O(n)，而列表的速度为 O(1)。这是因为每次向元组添加内容时，我们都必须分配和复制整个元组，而对于列表来说，只有当额外的余量用完时才需要这样做。因此，不存在类似就地追加的操作；添加两个元组总是返回一个新的元组，而这个新的元组位于内存中的一个新位置。

>>> t = (1, 2, 3, 4)
>>> t[0] = 5
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: 'tuple' object does not support item assignment

不存储用于调整大小的额外余量的好处是可以减少资源的使用。使用任何追加操作创建的大小为 100,000,000 的列表实际使用了 104,391,068 个元素的内存，而持有相同数据的元组只使用了 100,000,000 个元素的内存（节省了 4.4% 的内存）。这使得元组变得轻量级，在数据变得静态时更受欢迎。

>>> t1 = (1, 2, 3, 4)
>>> t2 = (5, 6, 7, 8)
>>> t1 + t2
(1, 2, 3, 4, 5, 6, 7, 8)

此外，即使我们创建的列表没有追加（因此没有追加操作带来的额外空间），它的内存容量仍会大于具有相同数据的元组。这是因为列表必须跟踪有关其当前状态的更多信息，才能有效地调整大小。虽然这些额外的信息很小（相当于一个额外的元素），但如果有几百万个列表在使用，这些信息就会增加。

我们可以通过在例 3-7 中添加元组来了解这一点。在例 3-8 中，我们添加了相应的代码，发现内存使用量比原来的列表理解路径少了 1.19 倍。这总共节省了 72 Mb，而这仅仅是通过将数据转换为元组而实现的，其代价是数据不可变（代码后面补）。

元组静态特性的另一个好处是 Python 在后台所做的事情：资源缓存。Python 是垃圾回收的，这意味着当一个变量不再被使用时，Python 会释放该变量所使用的内存，将其还给操作系统，供其他应用程序使用（或用于其他变量）。然而，对于大小为 0-20 的元组，当它们不再被使用时，空间并不会立即还给系统：每种大小的元组最多会被保存 2000 个，以供将来使用。这意味着，当将来需要新的这种大小的元组时，我们不需要与操作系统通信，就能在内存中找到一个区域来放入数据，因为我们已经有了可用内存储备。不过，这也意味着 Python 进程会有一些额外的内存开销。

Python 也会缓存其他对象（一种称为 “freelist ”的机制）；但使用情况不同。当一个对象在 Python 代码中被销毁并被设置为垃圾回收时，Python 会将其保留在自由列表中，这样新对象就可以更快地被实例化和分配。然而，对于非元组对象，这些 freelist 要比元组 freelist 小得多，其性能优势主要体现在 Python 解释器的内部工作中。在 CPython 3.12.2 中，各种对象的 freelist 的大小如下：

• 生成器 80
• 上下文 255
• 字典 80
• 浮点数 100
• 列表：80
• 元组 40,000 个（1-20 号元组的每种大小各 2,000 个）

虽然这看似是一个很小的好处，但却是元组的神奇之处：元组可以轻松快速地创建，因为元组可以避免与操作系统通信，而这可能会耗费程序大量的时间。例 3-9 显示，实例化 list 比实例化元组要慢几倍–如果在快速循环中进行实例化，那么时间会很快增加！

• 例 3-9. 列表与元组的实例化时间比较

In [1]: %timeit l = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
21.8 ns ± 4.63 ns per loop (mean ± std. dev. of 7 runs, 10,000,000 loops each)

In [2]:  %timeit t = (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
6.51 ns ± 0.0396 ns per loop (mean ± std. dev. of 7 runs, 100,000,000 loops each)

3.3 总结

当数据已有内在排序时，列表和元组是快速、低开销的对象。这种固有的排序方式可以避开这些结构中的搜索问题：如果事先知道排序方式，则查找的速度为 O(1)，搜索的速度为 O(log n)。如果事先不知道顺序，我们就必须进行昂贵的 O(n) 线性搜索。虽然可以调整列表的大小，但必须注意正确理解发生了多少总体分配，以确保数据集仍能容纳在内存中。另一方面，元组可以快速创建，而且不会增加列表的开销，但代价是不可修改。我们讨论了如何预分配列表，以减轻频繁追加 Python 列表所带来的一些负担，我们还研究了其他有助于解决这些问题的优化方法。

在下一章中，我们将介绍字典的计算特性，它可以解决无序数据的搜索/查找问题，但代价是开销。