题⽬描述

输⼊⼀个整数，输出该数 32 位⼆进制表示中 1 的个数。其中负数⽤补码表示。

示例1
输⼊：10
返回值：2
说明：⼗进制中10的32位⼆进制表示为0000 0000 0000 0000 0000 0000 0000 1010，其中有两个1。

示例2
输⼊：-1
返回值：32
说明：负数使⽤补码表示 ，-1的32位⼆进制表示为1111 1111 1111 1111 1111 1111 1111 1111，其中32个1

思路及解答

错误解答（不考虑负数）

⾸先说⼀个错误的解法，很多⼈可能会想到，那就是不断对 2 取余数。但是这种做法有个致命的缺陷，那就是忽略了负数，负数使⽤补码表示的时候，是取反之后加⼀

public class Solution {
	public int NumberOf1(int n) {
		int num = 0;
		while (n != 0) {
			int tmp = n % 2;
			if (tmp == 1||tmp==-1) ++num;
			n /= 2;
		}
		return num;
	}
}

字符串遍历

将整数转换为二进制字符串，然后遍历字符串统计’1’的个数。

public int NumberOf1(int n) {
    String binaryStr = Integer.toBinaryString(n);
    int count = 0;
    for (int i = 0; i < binaryStr.length(); i++) {
        if (binaryStr.charAt(i) == '1') {
            count++;
        }
    }
    return count;
}

• 时间复杂度：O(n)，n为二进制位数（固定32位）
• 空间复杂度：O(n)，需要存储二进制字符串

API调⽤(不推荐)

Java标准库提供了统计二进制1个数的方法。

public int hammingWeight(int n) {
    return Integer.bitCount(n);
}

位掩码与移位（逐位检查）

使用位掩码和移位操作逐位检查是否为1。

移位算法，把整数当成⼆进制，不断向右移位和1 进⾏与计算。利⽤了所有数和1 进⾏与计算，结果为1则证明最后⼀位是1 。

public int NumberOf1(int n) {
    int count = 0;
    int mask = 1;
    for (int i = 0; i < 32; i++) {
        if ((n & mask) != 0) {
            count++;
        }
        mask <<= 1;
    }
    return count;
}

无符号右移：

public int NumberOf1(int n) {
    int count = 0;
    while (n != 0) {
        count += (n & 1);
        n >>>= 1; // 无符号右移
    }
    return count;
}

位运算

利用n & (n – 1)可以消除最右边的1的特性，直到n变为0

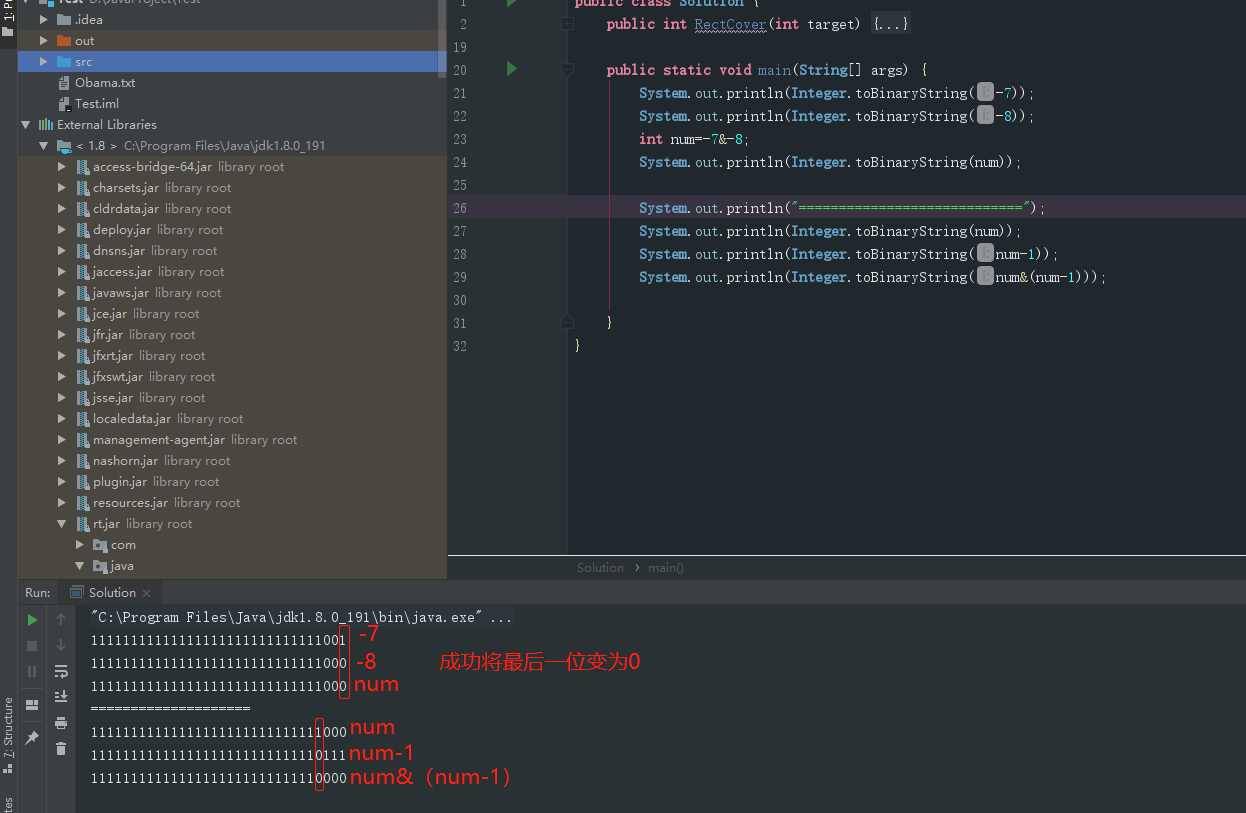
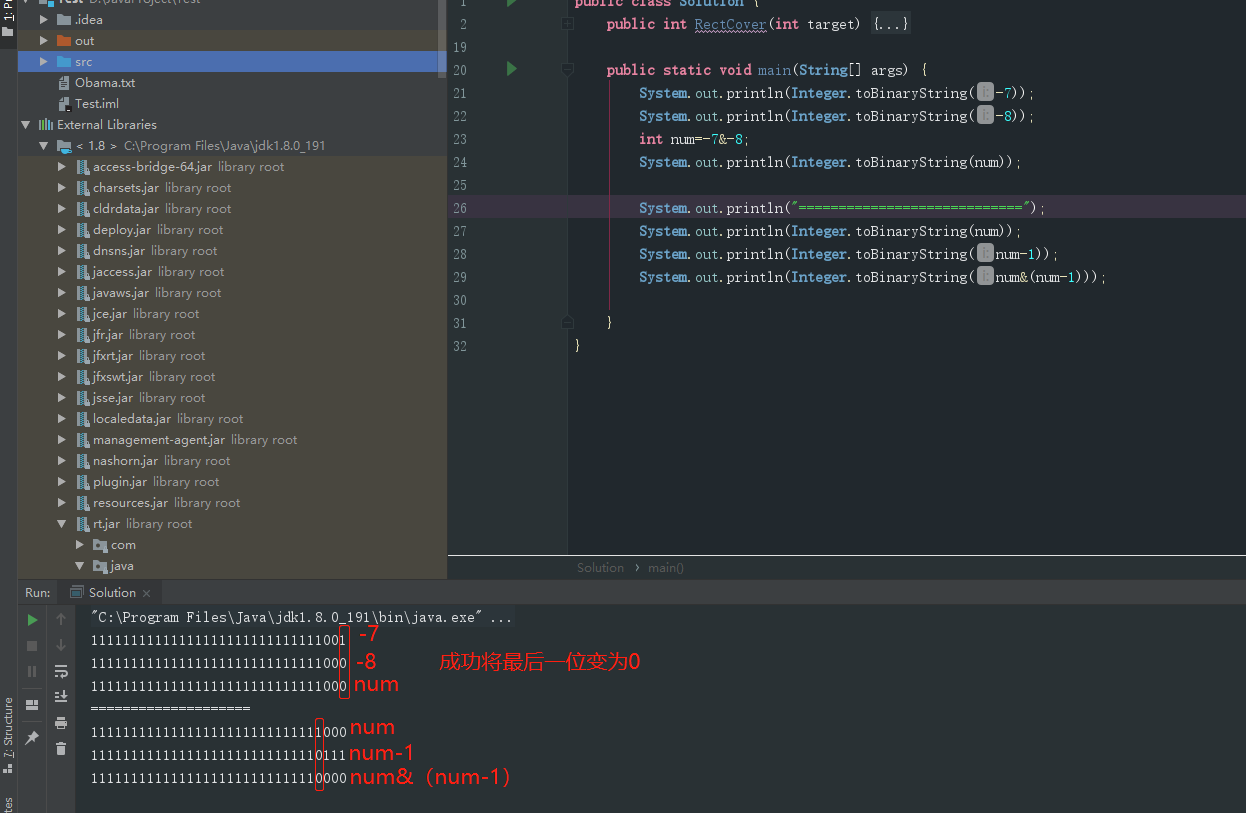
⽐如7的⼆进制是111 ，那么7&6=111&110=110=6 ，就完美把最后⼀位1 变成0 了， 6 的⼆进制是110 , 6&5=110&101=100=4 ，也把最后⼀位1 变成了0 。

负数呢？⽐如：
32位-7 = 11111111111111111111111111111001 ，
32位-8 = 11111111111111111111111111111000，
-7&-8 = 11111111111111111111111111111000

public class Solution {
    public int NumberOf1(int n) {
        int num = 0;
        while (n != 0) {
            num++;
            n &= (n - 1);
        }
        return num;
    }
}