
特征点法前端
目录
\(\quad\)前端又称为视觉里程计 (VO),它根据相邻图像间的信息来估计出相机的运动。估计值既可作为结果输出,也可以作为初始值提供给后端来进行优化。VO 的实现,按照是否提取图像特征,分为特征点法前端和直接法前端。
1.0 特征点与特征点匹配
\(\quad\)如前所述,VO 的主要问题是根据图像信息来估计相机的运动。一般来说,我们首先从图像中选取出比较有代表性的点,然后根据这些点来估计相机的位姿(和点的定位)。在SLAM 中,这些点也称为路标。
1.1 特征点
\(\quad\)影像在计算机中是以数值矩阵的方式来进行存储的。因此,单个像素也是一种特征。但我们希望所提取的特征能够在相机运动后保持稳定,即有一定程度的不变性。而单个像素往往收到光照、视角、形变等等因素的影响而变得不稳定。因此,在计算机视觉中,常常通过人工设计的特征提取器来获取具有鲁棒性的图像特征。
\(\quad\)常见的图像特征就是角点。角点有易辨认,易提取的特点。但它也存在一些问题。比如距离的影响:从远处看是角点的地方,相机移近之后却不是了。还有旋转的影响:相机旋转后,不同影像上的同一角点可能就具有不同的外观。
\(\quad\)为此,研究者们设计了许多能够提取具有足够鲁棒性特征提取算法,如 SIFT, SURE, ORB 等等。这些人工设计的特征点一般都具备如下性质:
- 可重复性:相同的特征点可以在不同的影像上找到;
- 可区别性:不同的特征点具有不同的表达;
- 高效率:同一图像中,特征点的数量远小于像素的数量;
- 本地性:提取的特征点仅仅和一小片图像区域相关。
\(\quad\)一个特征点由关键点 (key-point) 和描述子 (descriptor) 两部分组成。关键点指的是该特征点在图像上的位置信息,有些还具有方向、大小等其他信息。描述子通常是一个向量,它按照某种人为设计的方式,描述了特征点周围像素点信息。描述子一个重要设计原则就是外观相似的特征具有相似的描述子。
\(\quad\)由于SLAM 是一种实时应用,因此除了鲁棒性之外,算法的实时性也应该被考虑。实际上,特征点提取和匹配占据了SLAM 主要的时间消耗。因此选用合适的特征提取算法至关重要。如 SIFT 算子虽好,但计算量太大,时间消耗过多。虽然大部分的特征提取都具有良好的并行性,可以使用 GPU 来加速运算,但由此带来的成本提升也要纳入考量。而ORB算子是质量和效率之间比较好的折中方案,常被用在目前的视觉 SLAM 方案中。
1.2 ORB
\(\quad\)网上关于 ORB 算子的资料很多,相关论文也可以直接获取。这里仅仅进行一个简要的叙述。
\(\quad\)ORB 特征一样由关键点和描述子两部分组成。它的关键点为 Oriented FAST,是 FAST 算子的一种改进;描述子则是BRIEF。
\(\quad\)FAST 算子很高效,但不具备尺度和旋转不变性。通过构建影像金字塔,在不同尺度的影像上提取特征来增加尺度不变性。然后引入像素重心来确定特征点的方向,引入旋转不变性。中间还可以使用Harris 角点滤波来提取出N 个最有可能的角点。
传统的BRIEF 描述子一样不具备旋转不变性,同样通过像素重心所确定的特征点方向来作为描述子点方向,得到steer BRIEF。最后,为了得到更好的两两比较模式,利用一个角点数据集和贪心算法得到一个具有高方差、低相关的模式,用以构建合适的描述子,称为 rBRIEF。
原论文ORB 在此。
1.3 特征匹配
\(\quad\)完成特征提取后,就可以进行特征匹配了。特征匹配解决了SLAM 中的数据关联问题,即确定了当前看到的路标和之前看到的路标之间的对应关系。
\(\quad\)最简单的特征匹配方法就是暴力匹配 (brute-force matching):计算待匹配特征点与其他特征点之间的距离,然后按距离排序,选取距离最近的特征点作为匹配点。在这里,描述子间的距离表示了两个特征点之间的相似程度,有欧式距离,汉明距离等等。对于特征点数量巨大的情况,快速近似最邻近 (FLANN) 算法会更为高效。
\(\quad\)接下来,我们希望根据匹配的特征点对来估计相机的运动。根据相机原理或所有的数据等不同,有三种情况:
- 当使用单目相机时,我们只知道二维的像素坐标,因此问题是根据两组匹配的 \(2D\) 点来估计相机运动。该问题用对极几何来解决。
- 当相机为双目或为RGB-D 相机时,由于我们可以获得深度信息,问题就是估计两组 \(3D\) 点间的运动。该问题用$ ICP $ 来解决。
- 如果有 \(3D\) 点云及其对应像素点的 \(2D\) 坐标,也能顾及相机运动。该问题通过 $PnP $求解。
2.0 对极几何
2.1 对极约束
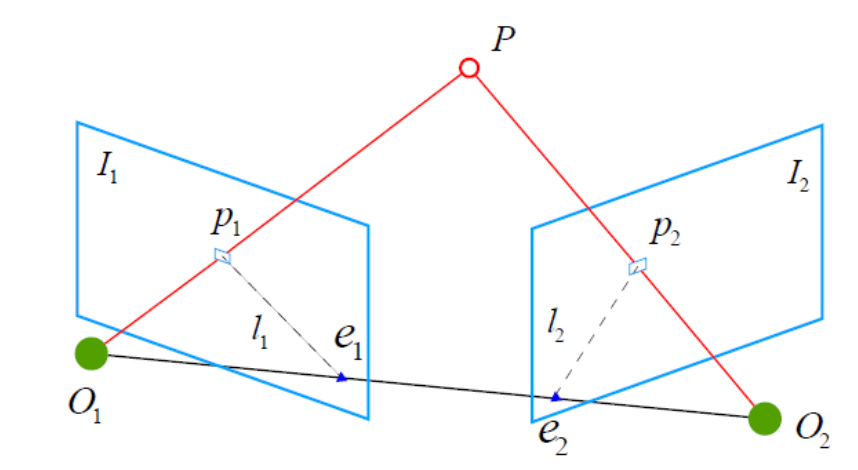
\(\quad\)上图展示了一对匹配好的特征点。我们希望求取这两帧之间的运动。设两个相机关心分别为 \(O_1\) 和 \(O_2\),第一帧到第二帧到运动为 \(R,t\)。点 $p_1 (x_1) $ 和点 $p_2 (x_2) $ 是同一个空间点在两个成像平面上的投影。连线 \(O_1 \ p_1\) 和 \(O_2 \ p_2\) 在三维空间中相交于点 \(P\)。这时,\(O_1, O_2\) 和 \(P\) 三点确定一个平面,称为极平面 (epipolar plane)。\(O_1, O_2\) 连线与像平面 $I_1, I_2 $ 的交点分别为 \(e_1, e_2\)。点 \(e_1, e_2\) 称为极点 (epipoles),是相机光心在另一幅影像上的投影。注意到这里 \(e_1, e_2\) 都位于像平面内。有时候它们有可能会落在成像平面之外。\(O_1, O_2\) 称为基线 (baseline)。而极平面与两个像平面之间的交线 \(l_1, l_2\) 为极线 (epipolar line),它们分别是射线 \(O_2 \ p_2\) 和 \(O_1 \ p_1\) 在对方影像上的投影。
\(\quad\)从几何上来看,射线 \(O_1 \ p_1\) 是像素点 \(p_1\) 所对应的物方点可能出现的位置:该射线上的所有点都有可能投影到点 \(p_1\) 上。射线 \(O_2 \ p_2\) 是像素点 \(p_2\) 所对应的物方点可能出现的位置。如果匹配正确的话,像素点 \(p_1, p_2\) 对应于同一个物方点。这两条射线的交点就是就是点 \(P\) 的空间位置。如果没有特征匹配,我们就必须在极线 \(l_2\) 上搜索 \(p_1\) 的匹配点。
现在我们从代数的角度上看,在第一帧的相机坐标系下,点 \(P\) 的空间位置为:
\[\mathbf{P}=[X, Y, Z]^T \]
根据针孔相机模型,不考虑畸变,两个像素点 \(p_1\), \(p_2\) 点像素(\(u,v\))坐标分别为:
\[s_1\mathbf{p}_1=\mathbf{K}\mathbf{P},\ s_2\mathbf{p}_2=\mathbf{K}(\mathbf{R}\mathbf{P}+\mathbf{t}) \]
\(s_1p_1\)和 \(p_1\)成投影关系,他们在齐次坐标系下是相等的,我们称这种关系为尺度意义下相等,记作:
\[sp\simeq p \]
在使用齐次坐标的时候,一个向量将等于它自身乘以一个非零的常数,这通常用于表达一个投影关系,\(s_1p_1=p_1\),这里可以参考一下14讲中P100页关于归一化平面和归一化坐标的定义:
- 归一化坐标可以看作相机前方 \(z=1\) 处的青面上的一个点,这个 \(z=1\) 的平面上的点也叫做归一化平面。归一化坐标再左乘内参即可得到像素坐标,所以我们可以将像素坐标 \((u,v)\) 看作是归一化平面上的点进行量化测量的结果
\[\mathbf{RP_w +t}=\underbrace{[X,Y,Z]^T }_{相机坐标系} \rightarrow \underbrace{[\frac{X}{Z},\frac Y Z ,1]}_{归一化坐标系} \]
我们再来看一下针孔相机的投影模型:
\[\begin{pmatrix} u\\ v\\ 1 \end{pmatrix} = \frac{1}{Z} \begin{pmatrix} f_x& 0 &c_x \\ f_y& 0 &c_y \\ 0 &0 &1 \end{pmatrix}\begin{pmatrix} X\\ Y \\ Z \end{pmatrix} \overset{\mathrm{def}}{=} \frac{1}{Z}KP \]
针孔相机的成像模型中本身对于\(Z\)就是未知的无约束的。
那么上述的两个投影关系可以写成:
\[p_1 \simeq KP,p_2\simeq K(RP+t) \]
这里,\(K\) 为相机内参矩阵。如果使用齐次坐标,则前面的系数 $s_1, s_2 $可以省略。设:
\[\mathbf{x}_1=\mathbf{K}^{-1}\mathbf{p}_1,\ \mathbf{x}_2=\mathbf{K}^{-1}\mathbf{p}_2 \]
这里,\(x_1\) 和 \(x_2\) 分别为两个像素点在各自相机坐标系下的归一化平面坐标。将之代入上式(将 \(p_1,p_2\) 分别带入上面的式子)可得:
\[\mathbf{x}_2 = \mathbf{R}\mathbf{x}_1+\mathbf{t} \]
这里本身笔者并不理解如何去除尺度因子之后仍然成立,于是接着带上尺度因子推倒了一遍,发现结果是一样的,也就是说尺度无法影响对极约束,当然求解出来的结果中的\(t\) 当然不是真实的尺度了,这里放出推倒过程:

将上式两边同时左乘\(\mathbf{t}^{\wedge}\),这相当于两侧同时和 $t $ 做外积:
\[\mathbf{t}^{\wedge}\mathbf{x}_2=\mathbf{t}^{\wedge}\mathbf{R}\mathbf{x}_1 \]
再将两侧同时左乘\(\mathbf{x}^T_2\):
\[\mathbf{x}^T_2\mathbf{t}^{\wedge}\mathbf{x}_2=\mathbf{x}^T_2\mathbf{t}^{\wedge}\mathbf{R}\mathbf{x}_1 \]
注意到\(\mathbf{t}^{\wedge}\mathbf{x}_2\) 是一个垂直于二者的向量,因此它和\(\mathbf{x}_2\) 的内积为0。由此可得:
\[\mathbf{x}^T_2\mathbf{t}^{\wedge}\mathbf{R}\mathbf{x}_1=0 \]
如果我们代入 $p_1, p_2 $ 则可得:
\[\mathbf{p}^T_2\mathbf{K}^{-T}\mathbf{t}^{\wedge}\mathbf{R}\mathbf{K}^{-1}\mathbf{p}_1=0 \]
这两个式子称为对极约束。它的几何意义为 $O_1, O_2 $和 \(\mathbf{P}\) 三点共面。这两个式子的中间部分分别称为本质矩阵 (essential matrix) \(\mathbf{E}\) 和基础矩阵 (fundamental matrix) \(\mathbf{F}\)。
\[\mathbf{E} = \mathbf{t}^{\wedge}\mathbf{R} \\ \mathbf{F} =\mathbf{K}^{-T}\mathbf{t}^{\wedge}\mathbf{R}\mathbf{K}^{-1} \\ \mathbf{x}_2^T\mathbf{E}\mathbf{x}_1=\mathbf{p}_2^T\mathbf{F}\mathbf{p}_1=0 \]
\(\quad\)对极约束给出了两个匹配点的空间位置关系。\(\mathbf{E}\) 和 \(\mathbf{F}\) 之间只差了相机内参。在 SLAM 中,相机内参一般都是已知的(也可以通过相机标定获得),所以实践中常常使用形式更简单的 \(\mathbf{E}\)。注意到 \(\mathbf{E}\) 完全由旋转矩阵 \(\mathbf{R}\) 和平移向量 \(\mathbf{t}\) 组成,由此我们也希望能够通过 \(E\) 来求得 \(\mathbf{R}\), \(\mathbf{t}\)。因此,相机位姿的估计就可以描述为:
- 通过匹配点求出 \(\mathbf{E}\);
- 根据E 求取 \(\mathbf{R}\), \(\mathbf{t}\)。
实际情况自然会比这个复杂。下面我们就来了解下这个求解过程。
2.2 本质矩阵
关于本大节(对极几何)的更详细的讲解和推导推荐看书 An Invitation to 3-D vision 的第五章。这章也正好是sample chapters 之一,可以免费阅读。地址在此Reconstruction from Two Calibrated Views .
本质矩阵 \(\mathbf{E} = \mathbf{t}^{\wedge} \mathbf{R}\) 是一个\(3 * 3\) 大小的矩阵,共 \(9\) 个未知数。它包含了一个相对位置信息 \(t\) 和一个旋转矩阵 \(R\)。所有本质矩阵也构成一个集合,具有以下的性质:
- 本质矩阵是由对极约束定义的。由上可知对极约束是一个等式为零的约束,所以对 \(E\) 乘以任意非零常数后,对极约束仍然满足。说明 \(E\) 在不同尺度下是等价的。
- 根据\(\mathbf{E} = \mathbf{t}^{\wedge} \mathbf{R}\),本质矩阵 \(E\) 的奇异值必定是\([\sigma,\sigma,0]^T\) 的形式。这称为本质矩阵的内在性质。想要详细的证明还请看上面的章样。
- 平易和旋转各自有 $3 \(个自由度,所以\)\mathbf{t}^{\wedge} \mathbf{R}$ 一共只有 \(6\) 个自由度。考虑到尺度等价性,本质矩阵 \(E\) 实际上只有\(5\)个自由度。
\(\quad\)既然 \(E\) 只有 \(5\) 个自由度,说明我们可以只用 \(5\) 对点来对其进行求解。但 \(E\) 的内在性质是非线性的,只用 \(5\) 对点求解会更麻烦些。考虑 \(E\) 的尺度等价性,可以使用 \(8\) 对点来求解 \(E\)。这就是八点法。
\(\quad\)考虑一对匹配点,它们的归一化坐标为\(\mathbf{x}_1 = [u_1, v_1,1]^T\) 和\(\mathbf{x}_2 = [u_2, v_2,1]^T\)。根据对极约束则有:
\[\begin{pmatrix} u_1, v_1, 1 \end{pmatrix} \begin{pmatrix} e_1 & e_2 & e_3 \\ e_4 & e_5 & e_6 \\ e_7 & e_8 & e_9 \\ \end{pmatrix} \begin{pmatrix} u_2 \\ v_2 \\ 1 \end{pmatrix} = 0 \]
把矩阵 \(E\) 展开,写成向量的形式 (stacked version):
\[\mathbf{e} =[ e_1, e_2, e_3, e_4, e_5, e_6, e_7, e_8, e_9]^T \]
对极约束就可以写成与 \(e\) 有关的线形形式:
\[[u_1u_2, u_1 v_2, u_1, v_1 u_2, v_1 v_2, v_1, u_2, v_2, 1] \mathbf{e} = 0 \]
\(8\)个特征点对就构成了一个线性方程组。设系数矩阵为 \(A\),它是一个 \(8 * 9\) 大小的矩阵,\(e\) 位于该矩阵的零空间 (Null Space) 中。如果矩阵 \(A\) 满足秩为 \(8\)(满秩)的条件(\(8\) 个点不共面),那么其零空间维度为 \(1\),即 \(e\) 构成一条线,这与 \(e\) 的尺度等价性是一致的。
求解出 \(E\) 后,问题就变成了如何从 \(E\) 中恢复出相机的运动 \(R,t\)。该过程可以由奇异值分解 (SVD) 得到。且对于任意一个本质矩阵 \(E\),有两组相对运动 \((R, t)\) 与之对应。同样地,详细证明请看上面的书籍章样。假设 \(E\) 的SVD 分解为:
\[\mathbf{E} = \mathbf{U} \mathbf{\Sigma} \mathbf{V}^T \]
其中,$U, V $ 是正交阵,\(\mathbf{\Sigma}\) 是奇异值矩阵。与 \(E\) 对应的两组 \((R, t)\) 分别为:
\[\begin{align} \mathbf{t}_1^{\wedge} = \mathbf{U} \mathbf{R}_z(\frac{\pi}{2}) \mathbf{\Sigma} \mathbf{U}^T, & \ \mathbf{R}_1 = \mathbf{U} \mathbf{R}^T_z(\frac{\pi}{2}) \mathbf{V}^T \\ \mathbf{t}_2^{\wedge} = \mathbf{U} \mathbf{R}_z(-\frac{\pi}{2}) \mathbf{\Sigma} \mathbf{U}^T, & \ \mathbf{R}_2 = \mathbf{U} \mathbf{R}^T_z(-\frac{\pi}{2}) \mathbf{V}^T \\ \end{align} \]
其中,\(\mathbf{R}_z(\frac{\pi}{2})\) 表示沿 \(z\) 轴旋转 \(90\) 度的旋转矩阵。对比上面两个式子可以发现,这两组解其实是以参考帧为中心,绕 \(z\) 轴呈 \(180\) 度旋转对称的两组解,如下图所示(来自上面推荐的书籍):
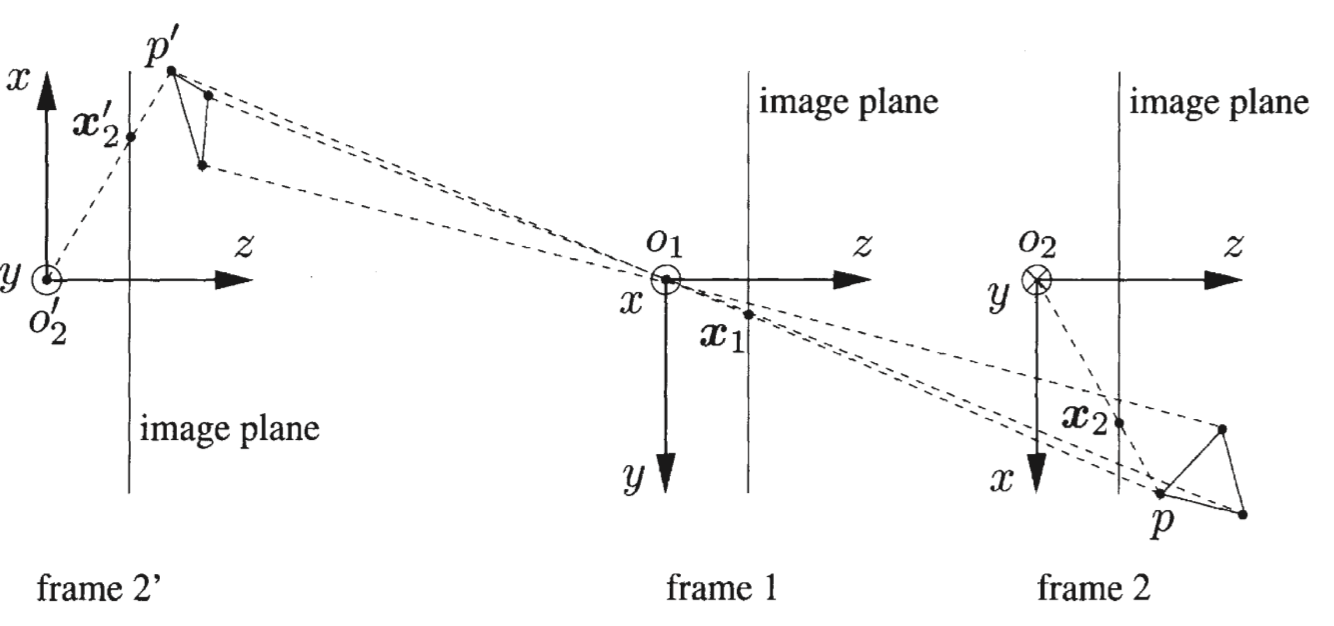
\(\quad\)同时,由于 \(E\) 可以取任意符号,即 \(-E\) 和 \(E\) 是等价的,所以对任意一个 \(t\) 取负号又取得一个符合条件的解,所以一共有四组符合条件的解。
\(\quad\)我们可以将任意一对特征点代入所取得的\(4\)组解中,检测该点在两个相机下的深度值。显然物方特征点应该位于两个相机的前方,取两个深度值都为正的解即是正确的解。
\(\quad\)最后,使用带有噪声的数据利用线形方程组求解得到的E 可能并不是一个”正确“的解,即奇异值矩阵并不满足 \(E\) 的内在性质 \(\mathbf{\Sigma} = diag(\sigma, \sigma, 0)\) 而是\(\mathbf{\Sigma} = diag(\lambda_1, \lambda_2, \lambda_3)\),为从大到小的排序。通常的做法是取\(\mathbf{\Sigma} = diag(\frac{\lambda_1 + \lambda_2}{2},\ \frac{\lambda_1 + \lambda_2}{2}, 0)\) 或者直接取 \((1, 1, 0)\)。
2.3 单应矩阵
\(\quad\)前面我们提到,利用八点法来求解本质矩阵的一个前提是系数矩阵满秩,这也意味着八组特征点不能(近似)落在同一个平面上。但在一些情况中,如无人机俯拍影像,这个假设就不成立了。此时,可以利用单应矩阵 (Homography) \(H\) 来求解相机运动。
\(\quad\)考虑图像 \(I1\) 和 \(I2\) 有匹配好的特征点对 \(p_1\) 和 \(p_2\),这些特征点所对应的物方点 \(P\) 落在同一平面上。以第一张影像的相机坐标系为惯性系,该平面的法向量为\(n\),到惯性系的原点的距离为 \(d\),则该平面可以表示为:
\[\mathbf{n}^T \mathbf{P}=d \]
整理得:
\[\frac{\mathbf{n}^T \mathbf{P}}{d} = 1 \]
影像 \(I2\) 相对于影像 \(I1\) 的运动为$ (R, t)$,则有:
\[\begin{align} \mathbf{P}_2 & = \mathbf{R} \mathbf{P}_1 + \mathbf{t} \\ & = \mathbf{R} \mathbf{P}_1 + \mathbf{t} \cdot \frac{\mathbf{n}^T \mathbf{P}_1}{d} \\ & = (\mathbf{R} + \frac{\mathbf{t} \mathbf{n}^T}{d}) \cdot \mathbf{P}_1 \end{align} \]
\(\quad\)这样,我们就得到了描述两个相机坐标系下同一物方点的转换关系,把中间括号内的部分抽取出来就得到了单应矩阵 \(H\)。当然,也可以在括号两端各加上相机矩阵 \(K\),得到\(\mathbf{K} (\mathbf{R} + \frac{\mathbf{t} \mathbf{n}^T}{d}) \mathbf{K}^{-1}\),这是高博书中的表示方式,描述了两个图像坐标之间的转换关系。
\(\quad\)单应矩阵包含了相机运动信息 \((R, t)\) 和对应平面的参数$ (n, d)$,同样是一个\(3 * 3\) 大小的矩阵,同样可以先通过匹配的特征点对计算 \(H\) 然后将之分解得到平移和旋转。值得注意的是,若相机运动为纯旋转,情形仍和单应矩阵相同,因为此时\(\mathbf{X}_2 = \mathbf{R} \mathbf{X}_1\) 或\(\mathbf{x}_1 = \mathbf{K} \mathbf{R} \mathbf{K}^{-1} \mathbf{x}_2\)。可见,旋转矩阵也是单应矩阵的一种。
由上可得:
\[\begin{pmatrix} u_2 \\ v_2 \\ 1 \end{pmatrix} = \begin{pmatrix} h_1 & h_2 & h_3 \\ h_4 & h_5 & h_6 \\ h_7 & h_8 & h_9 \\ \end{pmatrix} \begin{pmatrix} u_1 \\ v_1 \\ 1 \end{pmatrix} \]
需要注意的是这里的等号是在一个非零因子下成立的(齐次坐标)。实际处理中常常乘以一个非零因子使得 \(h_9 = 1\)。然后去掉这个非零因子可得:
\[u_2 = \frac{h_1 u_1 + h_2 v_1 + h_3}{h_7 u_1 + h_8 v_1 + h_9} \\ v_2 = \frac{h_4 u_1 + h_5 v_1 + h_6}{h_7 u_1 + h_8 v_1 + h_9} \]
整理得:
\[h_1 u_1 + h_2 v_1 + h_3 – h_7 u_1 u_2 – h_8 v_1 u_2 = u_2 \\ h_4 u_1 + h_5 v_1 + h_6 – h_7 u_1 v_2 – h_8 v_1 v_2 = v_2 \]
如此,一组匹配点可以构造出两个约束(三组约束中只有两组线性独立)。于是,自由度为 \(8\) 的单应矩阵可以由4对特征点算出(不存在三点共线的情况)。 这种将 \(H\) 转化为向量形式来直接求解的方式称为直接线性变换 (Direct Linear Transform, DLT)。
和本质矩阵的分解类似,分解单应矩阵H 也会得到4组解(如下所示)。这里的推导比较复杂(我也没看得很明白),还请参看前面的书籍章样。利用物方点的深度值为正(位于相机前方)的特性,可以排除两组解,剩下的两组解则需通过其他先验信息进行验证。
3.0 补充
3.1 尺度不确定性
\(\quad\)前面提到,\(E\) 具有尺度等价性,由它分解得到的 \((R, t)\) 也具有一个尺度等价性,但由于旋转矩阵 \(R\) 自身带有约束(行列式为 \(1\) 等),所以只有 \(t\) 具有一个尺度。换言之,分解 \(E\) 得到的其实是 \(qt\), q 为一个分零因子。而在通过分解 \(H\) 得到 \((R, t)\) 的时候,由于平面到坐标原点的距离未知,得到的 \(t\) 同样具有一个尺度等价性。在这种情况下,通常是将 \(t\) 进行归一化处理,即令其模长为 \(1\).
\(\quad\)对 \(t\) 长度的归一化直接导致了单目视觉的尺度不确定性。如果对轨迹和地图同时缩放任意倍数,我们得到的图像仍然是一样的。而对两张图像间的平移 \(t\) 进行归一化相当于固定尺度。以 \(t\) 的长度作为为单位长度,计算相机轨迹和特征点的三维位置。这被称为单目 slam 的初始化。初始化后,就可以利用 3D - 2D 来计算相机运动了。进行初始化的两张图像必须有一定程度的平移,而后都将以此步的平移为单位。
3.2 纯旋转
\(\quad\)在只有纯旋转的情况下,我们可以通过 \(H\) 来求取旋转。此时由于 \(t = 0\),\(E\) 也为 \(0\)。但此时我们无法利用三角测量来计算特征点的空间位置(不构成对极几何)。所以,单目初始化不能只有纯旋转,必须有一定程度的平移。
3.3 多余匹配
求解 \(E\) 和 \(H\) 都只需要用到少量的特征点对。而通过特征提取和匹配,往往能获得远超需要的特征点对。拥有这么多匹配点,在求解 \(E\) 或 \(H\) 的过程中当然可以构造一个最小二乘问题。但是,在可能存在误匹配的情况下,随机采样一致性 (RANSAC) 更受青睐。
