在Manim库中，FunctionGraph、ImplicitFunction和ParametricFunction都是用于绘制函数图像的类，但它们的适用场景、输入形式和实现方式有显著区别。

以下是详细对比：

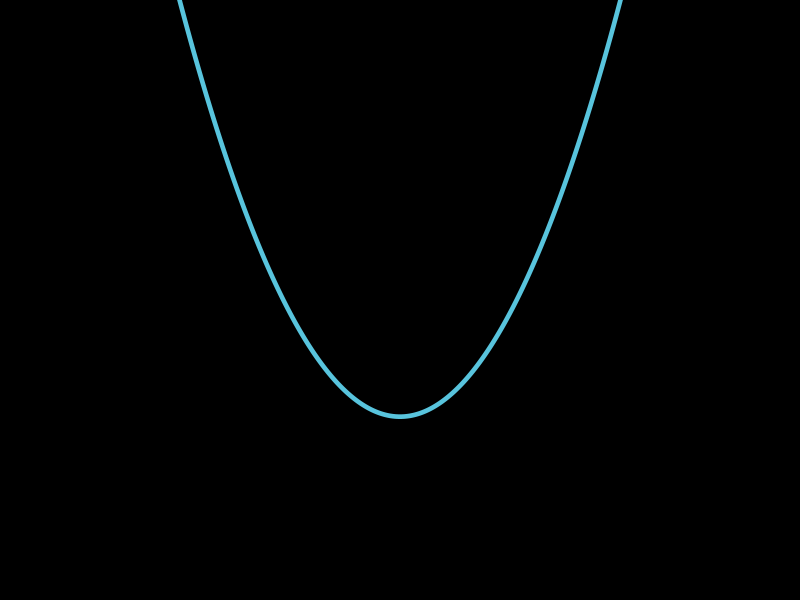
1. FunctionGraph

• 用途：绘制 显式函数 ($ y = f(x) $) 的图像（单值函数）。
• 输入要求：
  接受一个 一元函数 ($ f(x) \() 和 (\) x $) 的范围（如x_range=[-2, 2]）。
• 特点：
  • 直接映射 ($ x \to (x, f(x)) $)。
  • 要求函数是 单值 的（一个$ x \(对应唯一\) y $)。
• 示例代码：

class Example(Scene):
    def construct(self):
        # 绘制 y = x^2
        graph = FunctionGraph(lambda x: x**2, x_range=[-2, 2], color=BLUE)
        self.add(graph)

2. ImplicitFunction

• 用途：绘制 隐函数 ($ F(x, y) = 0 $) 的图像（如圆、椭圆）。
• 输入要求：
  接受一个 二元函数 ($ F(x, y) \() 和 (\) x, y $) 的范围（如x_range=[-3, 3], y_range=[-3, 3]）。
• 特点：
  • 通过数值方法（如Marching Squares算法）求解满足 ($ F(x, y) = 0 $) 的点集。
  • 可绘制 多值曲线（如一个$ x \(对应多个\)y ))。
• 示例代码：

class ImplicitFunctionExample(Scene):
    def construct(self):
        # 笛卡尔叶形线隐函数方程: x^3 + y^3 - 3axy = 0 (取 a=1)
        cartesian_leaf = ImplicitFunction(
            lambda x, y: x**3 + y**3 - 3 * x * y,  # F(x,y) = x³ + y³ - 3xy
            x_range=[-2, 2],
            y_range=[-2, 2],
            color=BLUE,
            stroke_width=3,
        )

        self.add(cartesian_leaf)

笛卡尔叶形线（一种自交曲线），可以展示隐函数处理 多值曲线 的能力（一个x对应多个y）。

3. ParametricFunction

• 用途：绘制 参数方程 定义的曲线（如螺旋线、摆线）。
• 输入要求：
  接受一个 向量值函数 ($ \mathbf{r}(t) = (x(t), y(t)) \() 和参数 (\) t $) 的范围（如t_range=[0, T]）。
• 特点：
  • 通过参数 ($ t $) 映射到点 $ (x(t), y(t)) $。
  • 可绘制 任意参数化曲线（包括封闭曲线、自交曲线）。
• 示例代码：

class ParametricFunctionExample(Scene):
    def construct(self):
        # 四叶玫瑰线参数方程: r = sin(2θ) 的笛卡尔形式
        # x = sin(2t)cos(t), y = sin(2t)sin(t)
        rose_curve = ParametricFunction(
            lambda t: np.array(
                [
                    np.sin(2 * t) * np.cos(t),  # x(t)
                    np.sin(2 * t) * np.sin(t),  # y(t)
                    0,
                ]
            ),
            t_range=[0, 2 * PI],  # 完整周期
            color=RED,
            stroke_width=4,
        )

        self.add(rose_curve)

四叶玫瑰线展示参数方程处理 封闭曲线 的能力，通过参数$ t $直接控制曲线生成过程。

4. 核心区别总结

特性	FunctionGraph	ImplicitFunction	ParametricFunction
输入形式	$ y = f(x) $	$ F(x, y) = 0 $	$ \mathbf{r}(t) = (x(t), y(t)) $
函数类型	显式函数（单值）	隐函数（多值）	参数方程
适用场景	简单函数（如 $ y = \sin x) $	复杂曲线（如椭圆、心形线）	任意参数化曲线（如螺旋线）
计算复杂度	低（直接计算）	高（数值求解）	中（采样计算）
多值支持	不支持	️ 支持	️ 支持

5. 如何选择？

• 用FunctionGraph当函数能显式写成$ y = f(x) $时（如多项式、三角函数）。
• 用ImplicitFunction当函数以方程 $ F(x, y) = 0 $ 给出时（如圆、椭圆）。
• 用ParametricFunction当曲线用参数 (t) 描述时（如摆线、贝塞尔曲线）。

通过理解这些差异，你可以根据函数的具体形式高效选择对应的Manim类进行绘制。