机器学习K-means算法在Python中的实现

作者：佚名 2017-09-12 16:57:43
人工智能
机器学习
算法 K-means是机器学习中一个比较常用的算法，属于无监督学习算法，其常被用于数据的聚类，只需为它指定簇的数量即可自动将数据聚合到多类中，相同簇中的数据相似度较高，不同簇中数据相似度较低。

K-means算法简介

K-means是机器学习中一个比较常用的算法，属于无监督学习算法，其常被用于数据的聚类，只需为它指定簇的数量即可自动将数据聚合到多类中，相同簇中的数据相似度较高，不同簇中数据相似度较低。

K-menas的优缺点：

优点：

• 原理简单
• 速度快
• 对大数据集有比较好的伸缩性

缺点：

• 需要指定聚类 数量K
• 对异常值敏感
• 对初始值敏感

K-means的聚类过程

其聚类过程类似于梯度下降算法，建立代价函数并通过迭代使得代价函数值越来越小

• 适当选择c个类的初始中心;
• 在第k次迭代中，对任意一个样本，求其到c个中心的距离，将该样本归到距离最短的中心所在的类;
• 利用均值等方法更新该类的中心值;
• 对于所有的c个聚类中心，如果利用(2)(3)的迭代法更新后，值保持不变，则迭代结束，否则继续迭代。

 

该算法的***优势在于简洁和快速。算法的关键在于初始中心的选择和距离公式。

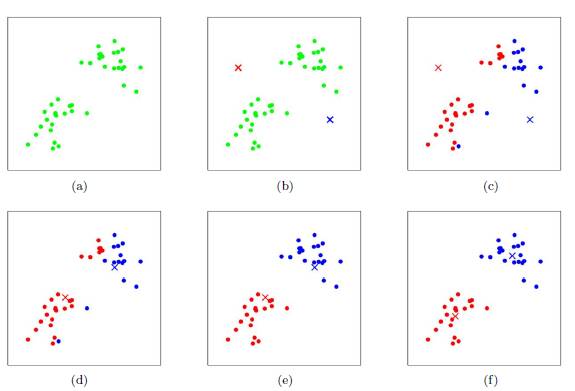
K-means 实例展示

python中km的一些参数：

  
 

   
  
sklearn.cluster.KMeans( 
   
  
 
   
  
    n_clusters=8, 
   
  
 
   
  
    init='k-means++', 
   
  
 
   
  
    n_init=10, 
   
  
 
   
  
    max_iter=300, 
   
  
 
   
  
    tol=0.0001, 
   
  
 
   
  
    precompute_distances='auto', 
   
  
 
   
  
    verbose=0, 
   
  
 
   
  
    random_state=None, 
   
  
 
   
  
    copy_x=True, 
   
  
 
   
  
    n_jobs=1, 
   
  
 
   
  
    algorithm='auto' 
   
  
 
   
  
    )  
  
 

• n_clusters: 簇的个数，即你想聚成几类
• init: 初始簇中心的获取方法
• n_init: 获取初始簇中心的更迭次数，为了弥补初始质心的影响，算法默认会初始10个质心，实现算法，然后返回***的结果。
• max_iter: ***迭代次数(因为kmeans算法的实现需要迭代)
• tol: 容忍度，即kmeans运行准则收敛的条件
• precompute_distances:是否需要提前计算距离，这个参数会在空间和时间之间做权衡，如果是True 会把整个距离矩阵都放到内存中，auto 会默认在数据样本大于featurs*samples 的数量大于12e6 的时候False,False 时核心实现的方法是利用Cpython 来实现的
• verbose: 冗长模式(不太懂是啥意思，反正一般不去改默认值)
• random_state: 随机生成簇中心的状态条件。
• copy_x: 对是否修改数据的一个标记，如果True，即复制了就不会修改数据。bool 在scikit-learn 很多接口中都会有这个参数的，就是是否对输入数据继续copy 操作，以便不修改用户的输入数据。这个要理解Python 的内存机制才会比较清楚。
• n_jobs: 并行设置
• algorithm: kmeans的实现算法，有：’auto’, ‘full’, ‘elkan’, 其中 ‘full’表示用EM方式实现

虽然有很多参数，但是都已经给出了默认值。所以我们一般不需要去传入这些参数,参数的。可以根据实际需要来调用。

下面展示一个代码例子 

  
 

   
  
from sklearn.cluster import KMeans 
   
  
 
   
  
from sklearn.externals import joblib 
   
  
 
   
  
from sklearn import cluster 
   
  
 
   
  
import numpy as np  
   
  
  
   
  
 
   
  
# 生成10*3的矩阵 
   
  
 
   
  
data = np.random.rand(10,3) 
   
  
 
   
  
print data 
   
  
 
   
  
# 聚类为4类 
   
  
 
   
  
estimator=KMeans(n_clusters=4) 
   
  
 
   
  
# fit_predict表示拟合+预测，也可以分开写 
   
  
 
   
  
res=estimator.fit_predict(data) 
   
  
 
   
  
# 预测类别标签结果 
   
  
 
   
  
lable_pred=estimator.labels_ 
   
  
 
   
  
# 各个类别的聚类中心值 
   
  
 
   
  
centroids=estimator.cluster_centers_ 
   
  
 
   
  
# 聚类中心均值向量的总和 
   
  
 
   
  
inertia=estimator.inertia_  
   
  
  
   
  
 
   
  
print lable_pred 
   
  
 
   
  
print centroids 
   
  
 
   
  
print inertia  
   
  
  
   
  
 
   
  
代码执行结果 
   
  
 
   
  
[0 2 1 0 2 2 0 3 2 0]  
   
  
  
   
  
 
   
  
[[ 0.3028348   0.25183096  0.62493622] 
   
  
 
   
  
[ 0.88481287  0.70891813  0.79463764] 
   
  
 
   
  
[ 0.66821961  0.54817207  0.30197415] 
   
  
 
   
  
[ 0.11629904  0.85684903  0.7088385 ]] 
   
  
 
   
  
0.570794546829  
  
 

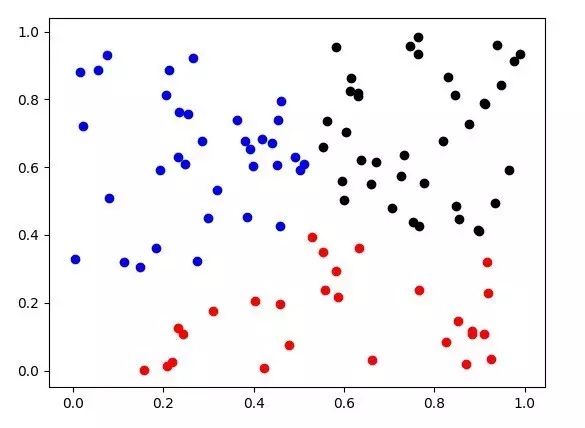
为了更直观的描述，这次在图上做一个展示，由于图像上绘制二维比较直观，所以数据调整到了二维，选取100个点绘制，聚类类别为3类 

  
 

   
  
from sklearn.cluster import KMeans 
   
  
 
   
  
from sklearn.externals import joblib 
   
  
 
   
  
from sklearn import cluster 
   
  
 
   
  
import numpy as np 
   
  
 
   
  
import matplotlib.pyplot as plt  
   
  
  
   
  
 
   
  
data = np.random.rand(100,2) 
   
  
 
   
  
estimator=KMeans(n_clusters=3) 
   
  
 
   
  
res=estimator.fit_predict(data) 
   
  
 
   
  
lable_pred=estimator.labels_ 
   
  
 
   
  
centroids=estimator.cluster_centers_ 
   
  
 
   
  
inertia=estimator.inertia_ 
   
  
 
   
  
#print res 
   
  
 
   
  
print lable_pred 
   
  
 
   
  
print centroids 
   
  
 
   
  
print inertia  
   
  
  
   
  
 
   
  
for i in range(len(data)): 
   
  
 
   
  
    if int(lable_pred[i])==0: 
   
  
 
   
  
        plt.scatter(data[i][0],data[i][1],color='red') 
   
  
 
   
  
    if int(lable_pred[i])==1: 
   
  
 
   
  
        plt.scatter(data[i][0],data[i][1],color='black') 
   
  
 
   
  
    if int(lable_pred[i])==2: 
   
  
 
   
  
        plt.scatter(data[i][0],data[i][1],color='blue') 
   
  
 
   
  
plt.show() 
  
 

 

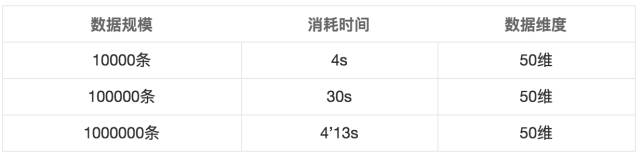
可以看到聚类效果还是不错的，对k-means的聚类效率进行了一个测试，将维度扩宽到50维

 

对于***的数据，拟合时间还是能够接受的，可见效率还是不错，对模型的保存与其它的机器学习算法模型保存类似

  
 

   
  
from sklearn.externals import joblib  
   
  
joblib.dump(km,"model/km_model.m")   
  
 

责任编辑：庞桂玉
来源： Python开发者
机器学习
K-means算法
Python